Consider Dijkstras algorithm:

Initialization

Same as MST-Prim, but also define a set S which is the complement of Q

Computing loop

while Q is nonempty

do u Extract-Min(Q)

S S {u}

for each vAdj[u]

do Relax(u, v, w)

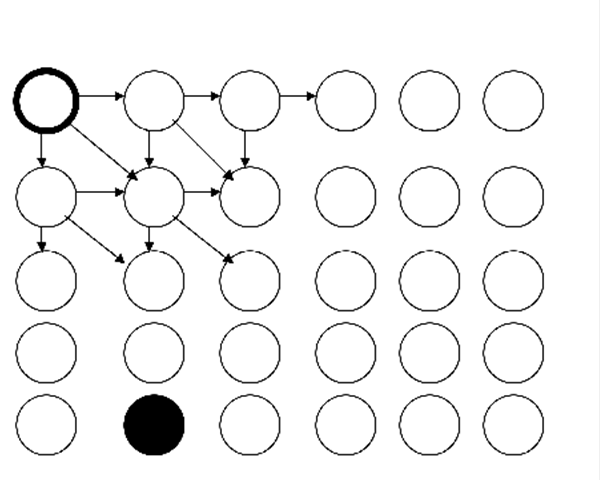
A) For the directed graph indicated by the sketch on the top, on exactly which iteration of the while loop is the shortest path distance from the top left vertex with the heavy line to the black vertex at location (5, 2)? Also, compute the shortest path distance to every vertex in the array.

(Assume that the sequence of arrows shown persists throughout all the vertices, and that each horizontal edge weight is set to exactly negative 2, each vertical edge weight is set to exactly 1, and each diagonal edge has weight 3. Break ties for Extract-Min lexicographically, for example, (2, 3) would come before (2, 5), if both had the same distance from the source estimate. We are asking at which point the estimate for the distance is the true minimum distance. This is different from asking at which iteration is the black node extracted. And, one last thing, you know that Dijkstras doesnt always work if there are negative weight edges in the graph. If it does work in this case, explain why. If is fails, show where.)

B)Now considering the same graph, but without the arrows, yet with the same edge weights. On which iteration of the while loop in Prims algorithm would the solid black vertex be extracted? Assume in the initialization that the upper left vertex is the root.