Consider the approximate integration of a function f(x) overthe interval [0,1]. Let M be a positive integer, and let h = 1/M, and xk = kh, for k = 0,1,2,3,,M. Thus x0 = 0 and xM = 1. Then one approximate integration formula is Implement these two methods in programs, and use each of these to approximately integrate the function f(x) = sin(x) over the interval [0,1], using successively the following values of M: M = 2, 4, 8, 16, . For each of these values of M print the error, i.e., the absolute value of the dierence between the approximation and the known exact value of the integral, which you can obtain analytically. Plot the results on the graphs. Make sure to represent to sucient precision in your program! Furthermore, for each of the two methods, determine from your computations the smallest value of M for which the error is less than 107. How many function evaluations are required in each of these two cases? Can you describe the observed behavior of the error? In particular, for each of the two methods, can you say approximately how the error depends on h ? More specically, it is known that the errors will be approximately proportional to hp, where p is an integer that depends on the method. Can you tell from the numerical results what p is for each of the two methods? Also can you explain what happens to the error when M gets very large? In the last part of this problem you will justify some of the previous results theoretically. Specically: (b) nd the error bound for the Simpson Rule, i.e. the upper bounds on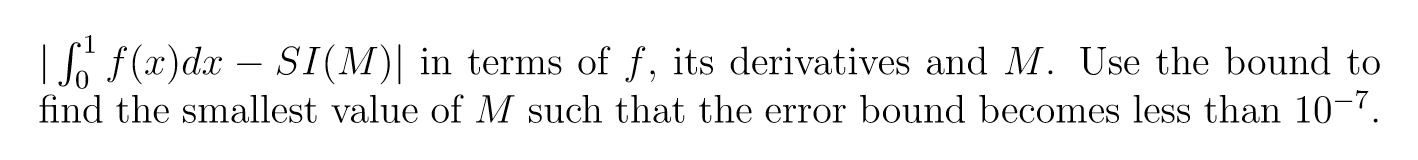

Please provide specific steps,thanks

I flade [autay+f+)+f(x=+5)+ ... +f(x-7)+=(n=1+) = MP(M) This method is known as the Midpoint Rule. Another approximate integration formula is . 1 f(x)da ~[(80)+4f(v1)+2f(02)+4f(73)+...+2f (zm=2)+4f (211)+f(zn)] = SI(M). This method, which requires M to be even, is known as the Simpson's Rule. (a) Use the internet, the calculus books or the textbook to find the upper bounds on the error of the Midpoint Rule, i.e., on | S. f(x)dx MP(M)| in terms of f, its derivatives and M. Use the bound to find the smallest value of M such that the error bound becomes less than 10-7. 1 S. f(x)dx SI(M)| in terms of f, its derivatives and M. Use the bound to find the smallest value of M such that the error bound becomes less than 10-7. I flade [autay+f+)+f(x=+5)+ ... +f(x-7)+=(n=1+) = MP(M) This method is known as the Midpoint Rule. Another approximate integration formula is . 1 f(x)da ~[(80)+4f(v1)+2f(02)+4f(73)+...+2f (zm=2)+4f (211)+f(zn)] = SI(M). This method, which requires M to be even, is known as the Simpson's Rule. (a) Use the internet, the calculus books or the textbook to find the upper bounds on the error of the Midpoint Rule, i.e., on | S. f(x)dx MP(M)| in terms of f, its derivatives and M. Use the bound to find the smallest value of M such that the error bound becomes less than 10-7. 1 S. f(x)dx SI(M)| in terms of f, its derivatives and M. Use the bound to find the smallest value of M such that the error bound becomes less than 10-7