Question: Consider the first order differential equation with initial condition t'+3t2y=2t, y(1)=16 where is a function of time t. 1 a. Show that y= +

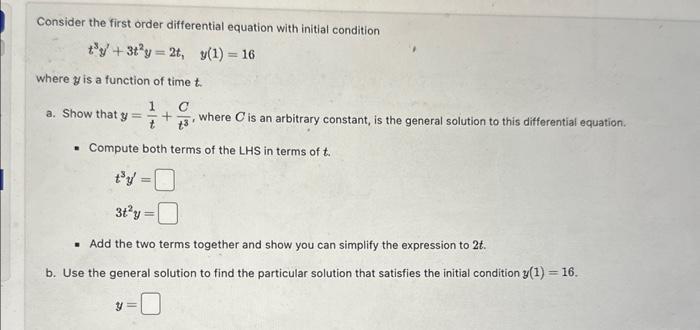
Consider the first order differential equation with initial condition t'+3t2y=2t, y(1)=16 where is a function of time t. 1 a. Show that y= + C +3 where C is an arbitrary constant, is the general solution to this differential equation. Compute both terms of the LHS in terms of t. ty= 3t2y == = Add the two terms together and show you can simplify the expression to 2t. b. Use the general solution to find the particular solution that satisfies the initial condition y(1) = 16. y =

Step by Step Solution

There are 3 Steps involved in it

1 Expert Approved Answer

Step: 1 Unlock

To solve the given firstorder differential equation and find the particular solution tha... View full answer

Question Has Been Solved by an Expert!

Get step-by-step solutions from verified subject matter experts

Step: 2 Unlock

Step: 3 Unlock

Students Have Also Explored These Related Mathematics Questions!

When the 2020 COVID-19 pandemic swept the globe, many people lost their jobs. During this period, physiological and security issues became much more important to these individuals than pursuing...

CANMNMM January of this year. (a) Each item will be held in a record. Describe all the data structures that must refer to these records to implement the required functionality. Describe all the...

Let A, B be sets. Define: (a) the Cartesian product (A B) (b) the set of relations R between A and B (c) the identity relation A on the set A [3 marks] Suppose S, T are relations between A and B, and...

On January 2, $217981 in 10-year, 5% bonds with a market interest rate of 9%, and interest payable semiannually, were issued for $185895. On June 30, bond interest was paid. On December 31, the...

Briefly explain how each of the following influences the tensile modulus of a semi crystalline polymer and why: (a) Molecular weight (b) Degree of crystallinity (c) Deformation by drawing (d)...

Discuss the external and internal forces that create the need for organizational change. T-789

Thomas-Britt Industries was founded by Matt Thomas in 1950 as a small machine shop that produced parts for the aircraft industry. The Korean War brought rapid growth to Thomas-Britt. By the end of...

Problem 3. (12 marks) Recall that in a binary tree each node has at most 2 children. Suppose T is a binary tree with T-n (i.e. has n nodes). For every node v we use L and R, to denote the left...

1. Which pricing tactics does each company utilize? Evaluate the effectiveness of each one of these tactics for the particular pizza chain. 2. How might the current price wars change the pricing...

If Pitt Enterprises uses the FIFO method of process costing, compute the equivalent units for direct materials and conversion respectively for May. Select one: a . 2 2 5 , 0 0 0 materials; 1 9 5 , 0...

"IT's About Business 7.3 Amazon's B2B Marketplace Amazon Business (www.business.amazon.com) is Amazon's e-commerce website that caters to the wholesale and distribution business-to-business (B2B)...

1. In studying the motion of a string, it is determined that the speed of the various points along the string is given by the function v(s, t,m) = 2a + 3t+4ys +6+2 km where s is the coordinate of...

1 Taylor has been hired by ABC Towing to maintain the grounds at their storage yard. Taylor is paid a set amount regardless of the hours worked, controls when and how the work is done, and offers...

How to manage the transportation of goods from the supplier? (2 slides) How can you deal with any delay in the shipping of goods? How can you insure visibility? (3 slides) What is your plan to deal...

Level 1: Modify the program to make the LED flash slow three times (1000 ms delay), then quickly three times. (100 ms delay)

Lott Company uses a job order cost system and applies overhead to production on the basis of direct labor costs. On January 1,2022 . Job 50 was the only job in process. The costs incurred prior to...

Describe the Operations (+,,*,/) that can cause negligible addition (NA), error magnification (EM), or subtractive cancellation (SC) in calculating ?((x^2)+1) - x . Give the range of where they might...

Are there steps in the Safety Analysis of the Incident that should be removed or added? If so, what are they?

In the summer of 2009, ExxonMobil decided to invest 600 million dollars on developing algae as an alternative fuel and their TV commercials on this initiative were recently shown (e.g., December...

Circle the correct answer. (a) The elementary reversible isomerization of A to B was carried out in a packed-bed reactor. The following profiles were obtained: Two trend graph are shown. The...

Covariance of estimated population totals in a cluster sample. Suppose a one-stage cluster sample is taken from a population of N psus, with inclusion probabilities i. Let tx and ty be the population...

Survey evidence is often introduced in court cases involving trademark violation and employment discrimination. There has been controversy, however, about whether non probability samples are...

a. Suppose we ignore the fpc of a model-based estimator. Find b. Prove (5.36). Then