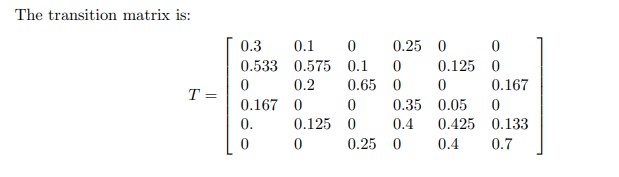
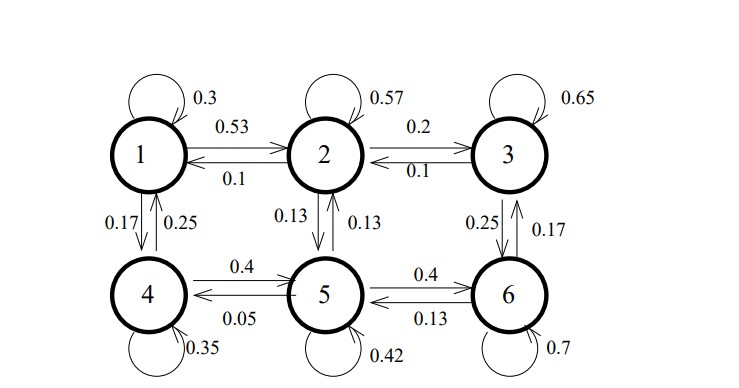
Consider the following game: You have a collection of coins of weighted coins of m different types. Specifically, coins of category i come up heads with probability pi , and you have ki of them. Therefore the total number of coins C = Pm i=1 ki . You also have an urn, which is initially empty. The coins are in a pile outside the urn. You now do the following. If either the urn or the outside is empty, pick a coin at random. If neither the urn nor the outside is empty, then pick either the urn or the outside with probability 1/2, and then pick a coin at random from the place that you have chosen. Flip the coin. If it comes up heads, then put it in the urn; if it comes up tails then put it outside. Keep doing this forever. This is a Markov process. The state of the system is determined by the number of coins of each category in the urn. Since there can be between 0 and ki coins of category i in the urn, the total number of states is q = (1 + k1) (1 + k2) . . .(1 + km) For example, suppose that there is 1 coin of category 1, which is a fair coin, and 2 coins of category 2, which have a 0.8 chance of coming up heads. Then there are 6 states: