Consider the following PDA, P, that recognizes the contextfree language L = {w {a, b} | w = w R}, i.e., all palindromes over the {a, b} alphabet:

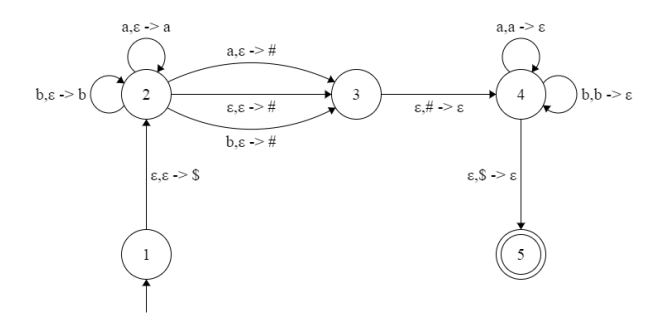
Recall the proof of Lemma 2.27 in the class-book (the proof that every PDA recognizes a certain CFL), and note that P is of such form that every transition either pops a symbol from the stack, or pushes a symbol on the stack (but does not do both), as required by the proof. Let GP be the grammar constructed as suggested by the proof of the Lemma. Provide a step-by-step derivation of a string baaab generated by PG. That is, show the steps A1,5 = u1 = . . . = uk = baaab, where A1,5 is the start variable in grammar GP . Note: you do not need to write out all the rules in the grammar GP , but only the ones needed for the derivation

a.c-> a a,a-> a.e-> # b,c-> b .E-> # bb-> b,c-> # E,E->$ E,S-> 4-11-)-111 ( 5 E. 3 111