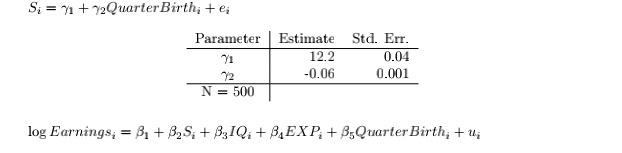
Consider the following regression: log Earnings; = B. +328+3310i + BEXP; +Hi where Earnings is the income they went on to earn after completing school S is the individual's years of schooling IQ is their intelligence EXP is the individual's work experience We should expect that B2 >0 since people with more schooling tend to earn higher wages. However, there is an obvious concern with endogeneity here; namely, people may choose to get more schooling in anticipation of higher earnings, and thus Earnings also causes S. Thus, we will need a instrument to use two staged least squares to obtain a consistent estimate of B2. (a) (6pts) Consider the following instruments for schooling S in the earnings regression. For each, argue whether or not you think it is relevant and exogenous. (i) IQ, the individual's intelligence (ii) The individual's proximity to a university growing up (iii) The individual's height (b) (7pts) You decide to use the variable Quarter Birthi, the quarter of an individual's birth, as an instrument for schooling, following Angrist and Krueger (1992). Your logic is that those born earlier in the school year (Fall) can turn 16 years old and drop out of highschool almost a whole year sooner than those born later (Spring). However, there is no systematic relationship between being born at a particular time in the year and having higher earnings. Based on the following regressions, do you believe that Quarter Birth is a valid instrument? (i.e., is it relevant and exogenous)? S = 71 +2Quarter Birth; +e; Parameter | Estimate Std. Err. 71 12.2 0.04 72 -0.06 0.001 N = 500 log Earnings; = 3, + 3,5; + B3IQ: + B, EXP + BsQuarter Birth; + 1; Parameter B. B. Bg B. Estimate Std. Err. 7.86 0.04 0.100 0.003 0.050 0.04 0.049 0.001 -0.80 1.28 N = 500 (c) (7pts) Here are the results of the first and second stage regressions: Stage 1: S; = 1 + Quarter Birth: + 7310i+ YEXP+u; Parameter Estimate Std. Err. 71 0.04 12.2 0.002 0.15 -0.56 0.0001 0.034 0.001 74 N = 500 Stage 2: log Earnings: = 81 +82%: +3,1Q+ 3,EXP: + 4; where is obtained from the first stage regression. Parameter Estimate Std. Err. 8. 7.29 0.008 8. 0.067 0.016 83 0.493 0.374 0.049 0.009 N = 500 Given the results of these regressions, do you believe that 32 = 0.067 is a good estimate of the true impact of schooling on earnings? Why or why not? Consider the following regression: log Earnings; = B. +328+3310i + BEXP; +Hi where Earnings is the income they went on to earn after completing school S is the individual's years of schooling IQ is their intelligence EXP is the individual's work experience We should expect that B2 >0 since people with more schooling tend to earn higher wages. However, there is an obvious concern with endogeneity here; namely, people may choose to get more schooling in anticipation of higher earnings, and thus Earnings also causes S. Thus, we will need a instrument to use two staged least squares to obtain a consistent estimate of B2. (a) (6pts) Consider the following instruments for schooling S in the earnings regression. For each, argue whether or not you think it is relevant and exogenous. (i) IQ, the individual's intelligence (ii) The individual's proximity to a university growing up (iii) The individual's height (b) (7pts) You decide to use the variable Quarter Birthi, the quarter of an individual's birth, as an instrument for schooling, following Angrist and Krueger (1992). Your logic is that those born earlier in the school year (Fall) can turn 16 years old and drop out of highschool almost a whole year sooner than those born later (Spring). However, there is no systematic relationship between being born at a particular time in the year and having higher earnings. Based on the following regressions, do you believe that Quarter Birth is a valid instrument? (i.e., is it relevant and exogenous)? S = 71 +2Quarter Birth; +e; Parameter | Estimate Std. Err. 71 12.2 0.04 72 -0.06 0.001 N = 500 log Earnings; = 3, + 3,5; + B3IQ: + B, EXP + BsQuarter Birth; + 1; Parameter B. B. Bg B. Estimate Std. Err. 7.86 0.04 0.100 0.003 0.050 0.04 0.049 0.001 -0.80 1.28 N = 500 (c) (7pts) Here are the results of the first and second stage regressions: Stage 1: S; = 1 + Quarter Birth: + 7310i+ YEXP+u; Parameter Estimate Std. Err. 71 0.04 12.2 0.002 0.15 -0.56 0.0001 0.034 0.001 74 N = 500 Stage 2: log Earnings: = 81 +82%: +3,1Q+ 3,EXP: + 4; where is obtained from the first stage regression. Parameter Estimate Std. Err. 8. 7.29 0.008 8. 0.067 0.016 83 0.493 0.374 0.049 0.009 N = 500 Given the results of these regressions, do you believe that 32 = 0.067 is a good estimate of the true impact of schooling on earnings? Why or why not