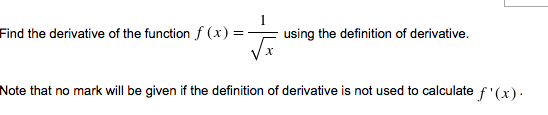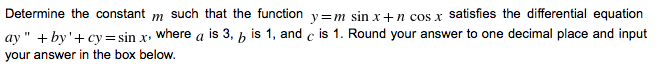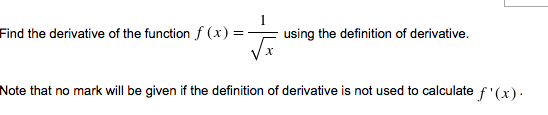
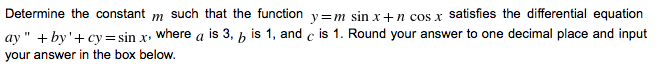
Consider the function f ( x) = tan -1( tan x ). Then f (0) =f (x) =0. Your professor claims that by the Mean Value Theorem, there is a number con (0, x) such that f(c) =0. (a) Prove your professor wrong by showing that there is no such a value of c. (b) Explain why your argument in (a) does not contradict the Mean Value Theorem.Find the derivative of the function f (x ) = - using the definition of derivative. Note that no mark will be given if the definition of derivative is not used to calculate f'(x) .Determine the constant m such that the function y=m sin x + n cos x satisfies the differential equation ay " + by'+ cy= sin x, where a is 3, , is 1, and c is 1. Round your answer to one decimal place and input your answer in the box below.Which of the following statement(s) is(are) true? O If f ( x ) is continuous at a, then the limit of f (x ) exists as x approaches d. O If the limit of f (x) exists as x approaches a, then f (x ) is continuous at a. O If f is continuous at a, then f is differentiable at a. O If f is differentiable at a, then f is continuous at a. O If f ( a ) is undefined, the limit of f (x) does not exist as x approaches (1. If f (x ) is differentiable at a, then the limit of f (x ) is lim f(ath) -f (a) A-0 h O The domain of f " can never be larger than that of f ' O If f (x ) is differentiable at a, then the limit of f (x) equals f (a ) .Consider the function x23 = 3y - sin (xx) 2/3(6-32) -35/3. (a) At x=0 ()-axis), find the smallest y value for this function. Show steps. (b) Find the equation of the line tangent to the graph of the function at the point found in (a). Show steps.Consider the function f (x)=etan -1 (x2+2v/2x+2). (a) Find all the asymptotes (if exist) via limits. Show steps. (b) Find the intervals of increases or decrease using the Increasing/Decreasing Test. Show steps. (c) Find the absolute maximum and minimum values (if exist) on the closed interval [ _ ]via the Closed Interval Method. Show steps. (d) Find the intervals of concavity and the inflection points using the Concavity Test. Show steps.Consider the function f (x) = ( sin x ) Inx. (a) (10 pts) Determine the domain of f (x ) . Show steps. (b) (5 pts) Calculate f ' (x) . Show steps. (c) (5 pts) Use the Mean Value Theorem to prove that there must be at least one point on at which the slope of the tangent line is equal to -3 (sin x/3) In (x/3) Show steps. 2n (d) (5 pts) Use the graph of f' (x ) to determine the exact number of such points on It described in (c). 3 Explain your process. (e) (5 pts) Use the graph of f ' (x ) to determine the number of inflection points on -, It . Explain your process.Find the value of ~ such that the line y=mx + c, where m is 8, is normal to the curve y=by x. where b is -12 and y is 8. Round your answer to three decimal places and input your answer in the box below