Answered step by step
Verified Expert Solution
Question
1 Approved Answer
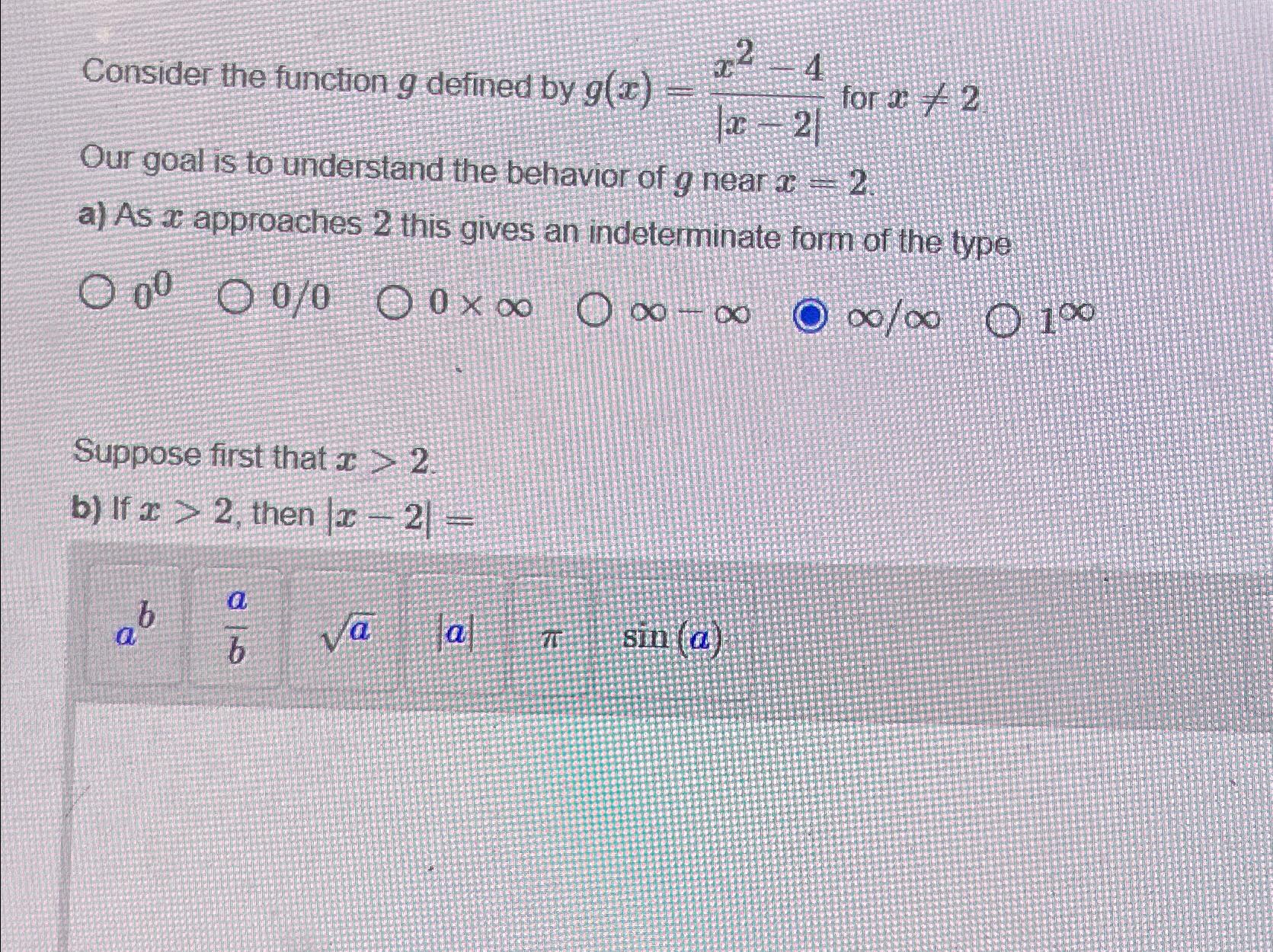
Consider the function g defined by g(x)=(x^(2)-4)/(|x-2|) for x!=2 Our goal is to understand the behavior of g near x=2 a) As x
Consider the function
gdefined by
g(x)=(x^(2)-4)/(|x-2|)for
x!=2\ Our goal is to understand the behavior of
gnear
x=2\ a) As
xapproaches 2 this gives an indeterminate form of the type\
0^(0)
(0)/(0)
0\\\\times \\\\infty
\\\\infty -\\\\infty
(\\\\infty )/(\\\\infty )
1^(\\\\infty )\ Suppose first that
x>2\ b) If
x>2, then
|x-2|=\
a^(b),(a)/(b),\\\\sqrt(a),|a,\\\\pi ,sin(a)|
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


