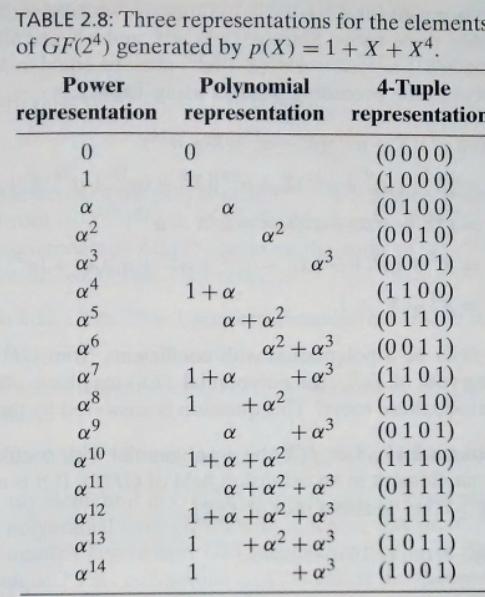
Consider the Galois field GF(24) given by Table 2.8. The element also a primitive element. Let go(X) be the lowest-degree polynomial over GF(2) that has a is = B, B, B, B4 as its roots. This polynomial also generates a double-error-correcting primitive BCH code of length 15. a. Determine go(X). b. Find the parity-check matrix for this code. c. Show that go(X) is the reciprocal polynomial of the polynomial g(X) that generates the (15, 7) double-error-correcting BCH code given in Example 6.1. TABLE 2.8: Three representations of GF(24) generated by p(X) = 1 + X+X4. Power representation 0 1 q Q3 Q4 as 96 97 98 99 a 0 Q1 a2 Q13 14 Polynomial representation 0 1 1+ 1 + a 1 92 a+a 1 1 + a 1+a+a a + a +q for the elements Q3 + + 1+++ ++ + + 4-Tuple representation (0000) (1000) (0100) (0010) (0001) (1100) (0110) (0011) (1101) (1010) (0101) (1110) (0111) (1111) (1011) (1001)