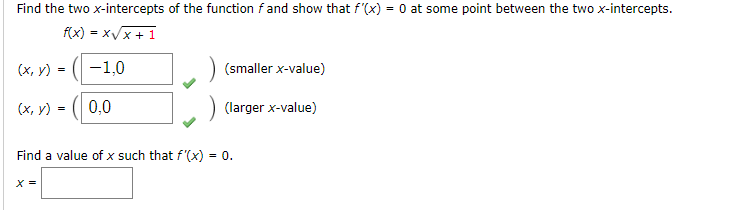Consider the graph of the function f (x) = x- - x - 20. (a) Find the equation of the secant line joining the points (-3, -8), and (5, 0). (b) Use the Mean Value Theorem to determine a point c in the interval (-3, 5) such that the tangent line at c is parallel to the secant line. C = (c) Find the equation of the tangent line through c.Determine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.) f(x) = 8 cos nX, [0, 2] Yes, Rolle's Theorem can be applied. O No, because f is not continuous on the closed interval [a, b]. O No, because f is not differentiable in the open interval (a, b). O No, because f(a) = R(b). If Rolle's theorem can be applied, find all values of c in the open interval (a, b) such that f'(c) = 0. (Enter your answers as a comma- separated list. If Rolle's Theorem cannot be applied, enter NA.) C =Determine whether Rolle's Theorem can be applied to f on the closed interval [a, b]. (Select all that apply.) f(x) = x2/3 - 2, [-64, 64] Yes, Rolle's Theorem can be applied. O No, because f is not continuous on the closed interval [a, b]. No, because f is not differentiable in the open interval (a, b). No, because f(a) = R(b). If Rolle's Theorem can be applied, find all values of c in the open interval (a, b) such that f (c) = 0. (Enter your answers as a comma- separated list. If Rolle's Theorem cannot be applied, enter NA.) C = 0 XDetermine whether the Mean Value theorem can be applied to f on the closed interval [a, b]. (Select all that apply.) f(x) = *+6 x - 1 [-9, 9] O Yes, the Mean Value Theorem can be applied. No, fis not continuous on [a, b]. O No, fis not differentiable on (a, b). O None of the above. If the Mean Value Theorem can be applied, find all values of c in the open interval (a, b) such that f(c) = f(b) - f(@) b - a (Enter your answers as a comma-separated list. If the Mean Value Theorem cannot be applied, enter NA.) C =Find the two x-intercepts of the function f and show that f(x) = 0 at some point between the two x-intercepts. f(x) = xx+1 (x, V ) = 1,0 (smaller x-value) (x, y ) = 0,0 (larger x-value) Find a value of x such that f'(x) = 0. X =