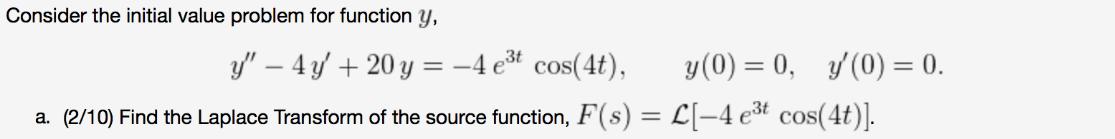
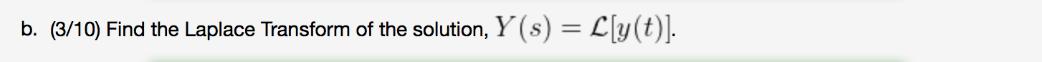
Consider the initial value problem for function y, y"-4y+20y= -4 et cos(4), y(0) = 0, y'(0) = 0. a. (2/10) Find the Laplace Transform of the source function, F(s) = L[-4 et cos(4t)]. b. (3/10) Find the Laplace Transform of the solution, Y(s) = L[y(t)]. Part 2/2. c. (5/10) A partial fraction decomposition for Y (s) found above is Y(s) = C's+D + As+B ((s - 3)+16) p(s) where A, B, C, D are constants and p(s) is the characteristic polynomial of the differential operator above. This partial fraction decomposition implies that the solution 1 to the differential equation above has the form y(t) = A fa(t) + B B(t) +C fc(t) + D d(t). Find the functions f, fB, fc, fD. You do not need to find the constants A, B, C, D. fa(t) = fB(t) = fc(t) = fD(t) =