Answered step by step
Verified Expert Solution
Question
1 Approved Answer
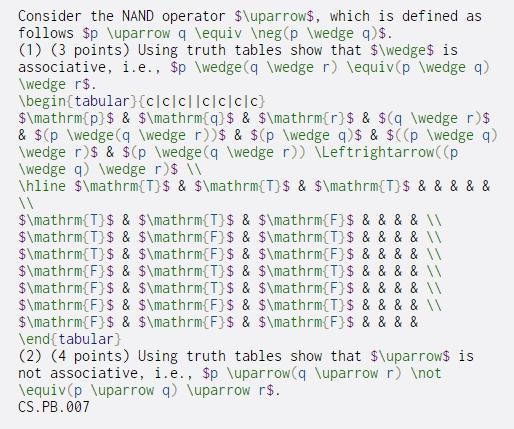
Consider the NAND operator $uparrows, which is defined as follows $p uparrow q equiv eg (p wedge q)$. (1) (3 points) Using truth tables show
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


