Consider the population of many adults. A researcher hypothesized that the average adult body temperature is lower than the often-advertised 98.6 degrees Fahrenheit. That is, the researcher wants to answer the question: "Is the average adult body temperature 98.6 degrees? Or is it lower?" To answer his research question, the researcher starts by assuming that the average adult body temperature was 98.6 degrees F. Then, the researcher went out and tried to find evidence that refutes the initial assumption. In doing so, the researcher selects a random sample of 130 adults. The average body temperature of the 130 sampled adults is 98.15 degrees with a standard deviation of 2.14.

a. What is the null hypothesis?

b. What is the alternative?

c. Calculate the t-statistic. What is the t-statistic?

d. What do you conclude

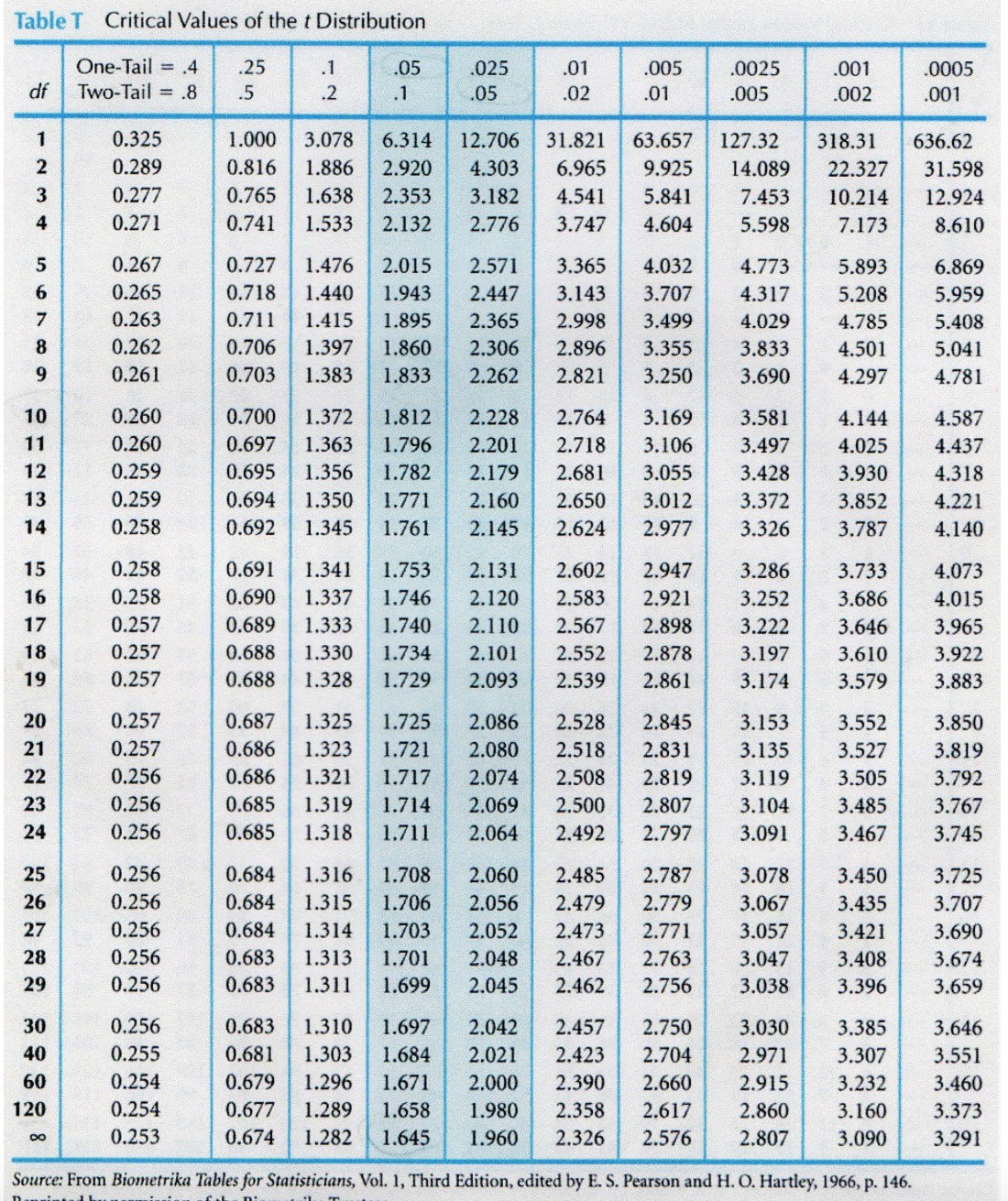
Table T Critical Values of the t Distribution One-Tail = .4 .25 .05 025 .01 .005 .0025 001 0005 df Two-Tail = .8 .5 N 1 .05 02 .01 .005 .002 001 0.325 1.000 3.078 6.314 12.706 31.821 63.657 127.32 318.31 636.62 0.289 0.816 1.886 2.920 4.303 6.965 9.925 14.089 22.327 31.598 AWN 0.277 0.765 1.638 2.353 3.182 4.541 5.841 7.453 10.214 12.924 0.271 0.741 1.533 2.132 2.776 3.747 4.604 5.598 7.173 8.610 0.267 0.727 1.476 2.015 2.571 3.365 4.032 4.773 5.893 6.869 0.265 0.718 1.440 1.943 2.447 3.143 3.707 4.317 5.208 5.959 0.263 0.711 1.415 1.895 2.365 2.998 3.499 4.029 4.785 5.408 0.262 0.706 1.397 1.860 2.306 2.896 3.355 3.833 4.501 5.041 0.261 0.703 1.383 1.833 2.262 2.821 3.250 3.690 4.297 4.781 10 0.260 0.700 1.372 1.812 2.228 2.764 3.169 3.581 4.144 4.587 11 0.260 0.697 1.363 1.796 2.201 2.718 3.106 3.497 4.025 4.437 12 0.259 0.695 1.356 1.782 2.179 2.681 3.055 3.428 3.930 4.318 13 0.259 0.694 1.350 1.771 2.160 2.650 3.012 3.372 3.852 4.221 14 0.258 0.692 1.345 1.761 2.145 2.624 2.977 3.326 3.787 4.140 15 0.258 0.691 1.341 1.753 2.131 2.602 2.947 3.286 3.733 4.073 16 0.258 0.690 1.337 1.746 2.120 2.583 2.921 3.252 3.686 4.015 17 0.257 0.689 1.333 1.740 2.110 2.567 2.898 3.222 3.646 3.965 18 0.257 0.688 1.330 1.734 2.101 2.552 2.878 3.197 3.610 3.922 19 0.257 0.688 1.328 1.729 2.093 2.539 2.861 3.174 3.579 3.883 20 0.257 0.687 1.325 1.725 2.086 2.528 2.845 3.153 3.552 3.850 21 0.257 0.686 1.323 1.721 2.080 2.518 2.831 3.135 3.527 3.819 22 0.256 0.686 1.321 1.717 2.074 2.508 2.819 3.119 3.505 3.792 23 0.256 0.685 1.319 1.714 2.069 2.500 2.807 3.104 3.485 3.767 24 0.256 0.685 1.318 1.711 2.064 2.492 2.797 3.091 3.467 3.745 25 0.256 0.684 1.316 1.708 2.060 2.485 2.787 3.078 3.450 3.725 26 0.256 0.684 1.315 1.706 2.056 2.479 2.779 3.067 3.435 3.707 27 0.256 0.684 1.314 1.703 2.052 2.473 2.771 3.057 3.421 3.690 28 0.256 0.683 1.313 1.701 2.048 2.467 2.763 3.047 3.408 3.674 29 0.256 0.683 1.311 1.699 2.045 2.462 2.756 3.038 3.396 3.659 30 0.256 0.683 1.310 1.697 2.042 2.457 2.750 3.030 3.385 3.646 0.255 0.681 1.303 1.684 2.021 2.423 2.704 2.971 3.307 3.551 0.254 0.679 1.296 1.671 2.000 2.390 2.660 2.915 3.232 3.460 120 0.254 0.677 1.289 1.658 1.980 2.358 2.617 2.860 3.160 3.373 0.253 0.674 1.282 1.645 1.960 2.326 2.576 2.807 3.090 3.291 Source: From Biometrika Tables for Statisticians, Vol. 1, Third Edition, edited by E. S. Pearson and H. O. Hartley, 1966, p. 146