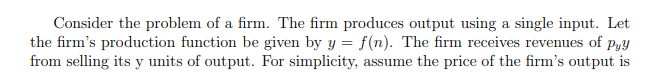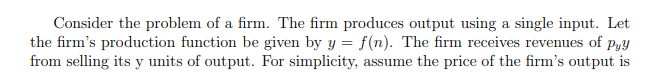
Consider the problem of a firm. The firm produces output using a single input. Let the firm's production function be given by y = f(n). The firm receives revenues of Pyy from selling its y units of output. For simplicity, assume the price of the firm's output is Py = 1. Let the firm's production function be strictly increasing and concave in n so that f'(n) > 0 and f"(n) Ps per unit. This allows the production firm to contract for delivery of n; units of the production input only in the state-of-nature in which the usual supplier is unable to fully deliver the n, purchased units of inputs. If the firm chooses to purchase n units of inputs from the intermediary it is required to pay pinj in costs at the time of delivery. However, not only is the unit price of inputs purchased from the intermediary higher than that of the supplier, but there is an addition unit cost of q that must be paid in advance - call this a contracting cost. The firm has no resources prior to selling any output so that any upfront costs it incurs from contracting for n, inputs from the intermediary and n, from its supplier must be financed by borrowing b units of resources from a lender. This loan must be sufficient to pay for the cost of contracted inputs. The lender charges an interest rater on the amount of money borrowed by the firm so that total repayments to the lender is in the amount (1+r)6.1 The timing is as follows: 1. The firm chooses how many units of the production input, ns, to purchase upfront from its supplier and how many units n, it wishes to contract for delivery from the intermediary that will arrive only in the event that the supplier cannot fully deliver the n, units of inputs. The firm borrows from the bank to pay for the cost png +ani. 2. Nature reveals whether the supplier fully delivers ns. If so, production occurs, output is sold and the bank is repaid principal and interest, (1 + r)b. Otherwise, the supplier delivers on, units of inputs, the intermediary delivers n, units of inputs, production occurs, the firm pays the intermediary pin for delivery of the n; inputs and the bank is repaid principal and interest, (1 + r)b As a technical condition, to ensure that a solution to this problem exists, assume that prices are such that (1+r)p. - [(1 7pi+(1+r)g] 6 > 0. a The problem of the firm can then be written as max {n [f(ns) (1+r)bs] + (1 7 ) [f(on: + ni) - pini - (1+r)bs]} na.na.ba subject to the constraint Pons + qn = b. Do the following: i Interpret the objective function of the firm in words. ii Interpret the constraint of the firm in words. iii Set-up the Lagrangean function for this problem. iv Construct all the relevant partial derivatives of the Lagrangean and set each of these partial derivatives equal to zero. v Combine the first-order conditions with respect to n, and b to construct an ng - b trade-off condition. Interpret this optimality condition in words. vi Combine the first-order conditions with respect to n and b to construct an ni - b trade-off condition. Interpret this optimality condition in words. vii Why would the production firm contract for delivery of inputs from the intermediary? Consider the problem of a firm. The firm produces output using a single input. Let the firm's production function be given by y = f(n). The firm receives revenues of Pyy from selling its y units of output. For simplicity, assume the price of the firm's output is Py = 1. Let the firm's production function be strictly increasing and concave in n so that f'(n) > 0 and f"(n) Ps per unit. This allows the production firm to contract for delivery of n; units of the production input only in the state-of-nature in which the usual supplier is unable to fully deliver the n, purchased units of inputs. If the firm chooses to purchase n units of inputs from the intermediary it is required to pay pinj in costs at the time of delivery. However, not only is the unit price of inputs purchased from the intermediary higher than that of the supplier, but there is an addition unit cost of q that must be paid in advance - call this a contracting cost. The firm has no resources prior to selling any output so that any upfront costs it incurs from contracting for n, inputs from the intermediary and n, from its supplier must be financed by borrowing b units of resources from a lender. This loan must be sufficient to pay for the cost of contracted inputs. The lender charges an interest rater on the amount of money borrowed by the firm so that total repayments to the lender is in the amount (1+r)6.1 The timing is as follows: 1. The firm chooses how many units of the production input, ns, to purchase upfront from its supplier and how many units n, it wishes to contract for delivery from the intermediary that will arrive only in the event that the supplier cannot fully deliver the n, units of inputs. The firm borrows from the bank to pay for the cost png +ani. 2. Nature reveals whether the supplier fully delivers ns. If so, production occurs, output is sold and the bank is repaid principal and interest, (1 + r)b. Otherwise, the supplier delivers on, units of inputs, the intermediary delivers n, units of inputs, production occurs, the firm pays the intermediary pin for delivery of the n; inputs and the bank is repaid principal and interest, (1 + r)b As a technical condition, to ensure that a solution to this problem exists, assume that prices are such that (1+r)p. - [(1 7pi+(1+r)g] 6 > 0. a The problem of the firm can then be written as max {n [f(ns) (1+r)bs] + (1 7 ) [f(on: + ni) - pini - (1+r)bs]} na.na.ba subject to the constraint Pons + qn = b. Do the following: i Interpret the objective function of the firm in words. ii Interpret the constraint of the firm in words. iii Set-up the Lagrangean function for this problem. iv Construct all the relevant partial derivatives of the Lagrangean and set each of these partial derivatives equal to zero. v Combine the first-order conditions with respect to n, and b to construct an ng - b trade-off condition. Interpret this optimality condition in words. vi Combine the first-order conditions with respect to n and b to construct an ni - b trade-off condition. Interpret this optimality condition in words. vii Why would the production firm contract for delivery of inputs from the intermediary