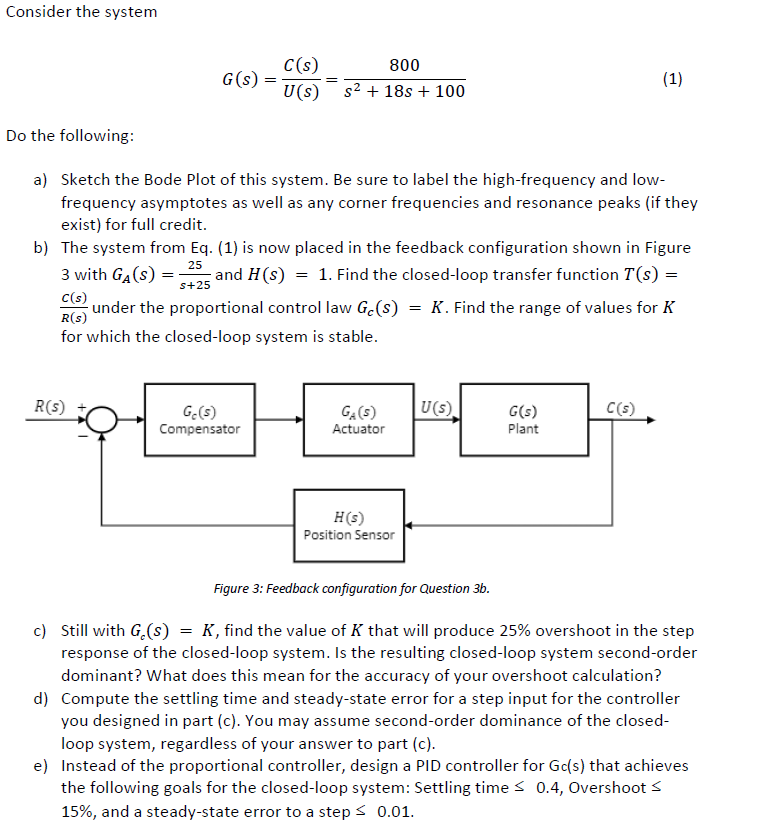
Consider the system G(s) C(s) U(s) = 800 s + 18s 100 (1) Do the following: a) Sketch the Bode Plot of this system. Be sure to label the high-frequency and low- frequency asymptotes as well as any corner frequencies and resonance peaks (if they exist) for full credit. b) The system from Eq. (1) is now placed in the feedback configuration shown in Figure 3 with GA(s) = and H(s) = 1. Find the closed-loop transfer function T(s) = C(s) R(s) 25 s+25 under the proportional control law Gc(s) for which the closed-loop system is stable. = K. Find the range of values for K R(s) G(s) Compensator GA(S) U(s) G(s) C(s) Actuator Plant H(s) Position Sensor Figure 3: Feedback configuration for Question 3b. c) Still with G,(s) = K, find the value of K that will produce 25% overshoot in the step response of the closed-loop system. Is the resulting closed-loop system second-order dominant? What does this mean for the accuracy of your overshoot calculation? d) Compute the settling time and steady-state error for a step input for the controller you designed in part (c). You may assume second-order dominance of the closed- loop system, regardless of your answer to part (c). e) Instead of the proportional controller, design a PID controller for Gc(s) that achieves the following goals for the closed-loop system: Settling time 0.4, Overshoot < 15%, and a steady-state error to a step < 0.01.