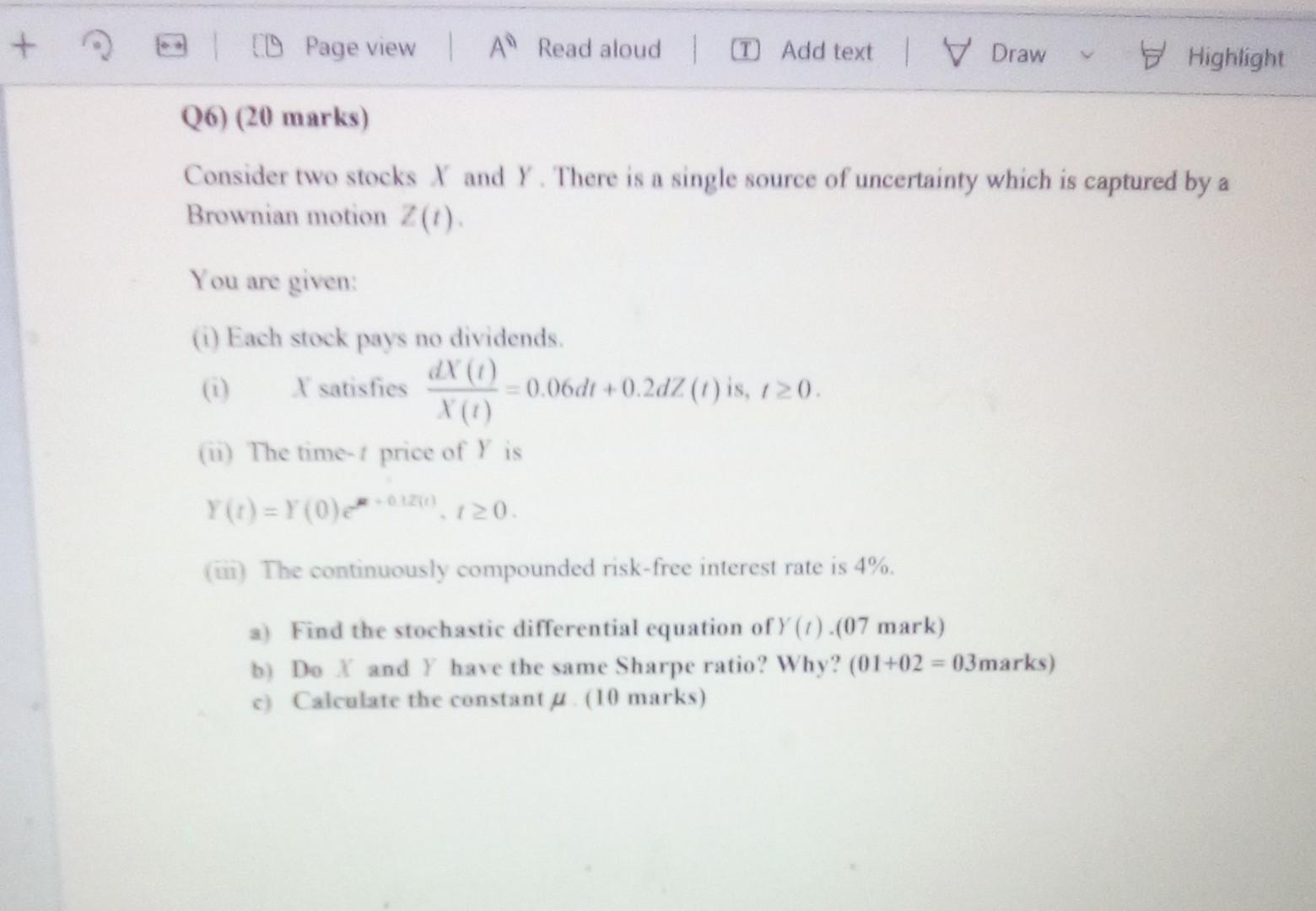
Consider two stocks X and Y. There is a single source of uncertainty which is captured by a Brownian motion Z(t). You are given: (i) Each stock pays no dividends. (i) X satisfies X(t)dX(t)=0.06dt+0.2dZ(t) is, t0. (ii) The time-t price of Y is Y(t)=Y(0)em+012(0),t0. (iii) The continuously compounded risk-free interest rate is 4%. a) Find the stochastic differential equation of Y(t).(07 mark) b) Do X and Y have the same Sharpe ratio? Why? (01+02=03 marks ) c) Calculate the constant . (10 marks) Consider two stocks X and Y. There is a single source of uncertainty which is captured by a Brownian motion Z(t). You are given: (i) Each stock pays no dividends. (i) X satisfies X(t)dX(t)=0.06dt+0.2dZ(t) is, t0. (ii) The time-t price of Y is Y(t)=Y(0)em+012(0),t0. (iii) The continuously compounded risk-free interest rate is 4%. a) Find the stochastic differential equation of Y(t).(07 mark) b) Do X and Y have the same Sharpe ratio? Why? (01+02=03 marks ) c) Calculate the constant . (10 marks)