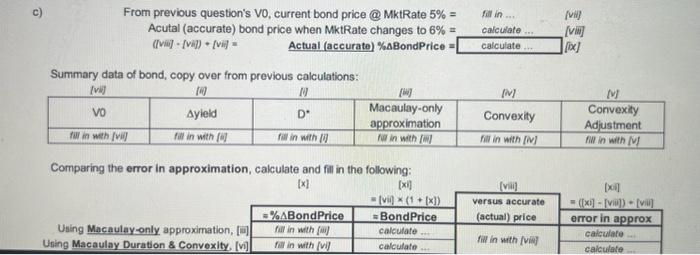
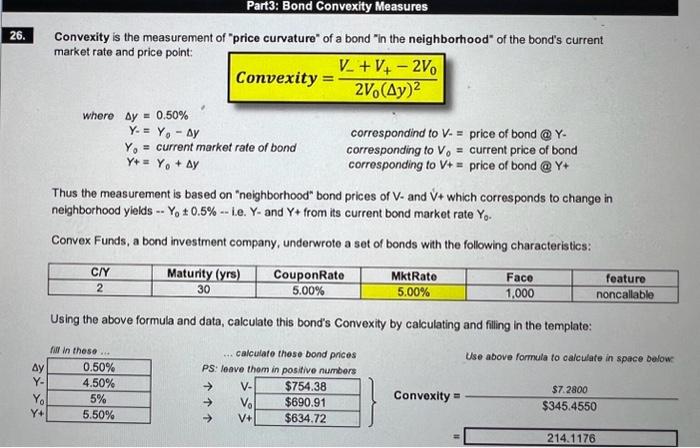
Continuing from previous question, use Modified Duration and Convexity to approximate the percentage change in price of the bond when its market rate change from 5% to 6%. PS; to save time, calculated for you, use a Macaulay Duration D of 15.8407. a) The "first order approximation" of \% BondPrice is a linear approximation. it uses Modified Duration in the following manner: Modified Duration D=1+C/YMktRateMacaulayDurationD Use the following template to fill in and calculate the following data: %BBondPrice%BBondPrice=Dyield=fillinnumbersbyshowingwork=eanswers The "second order approximation" of \% BondPrice is to incorporate the bond"s Convexity measurement: %BondPriceDyield+ConvexityAdjustment Use the following template to calculate and fill in the following data: From previous question's V0, current bond price @ MktRate 5%= fill in ... (Niif] Acutal (accurate) bond price when MiktRate changes to 6%= calculate ... [viii] (Iviii) - (vi) + / (i) = Actual (accurate) %B BondPrice = | [ix] Summary data of bond, copy over from previous calculations: Comparing the error in approximation, calculate and fill in the following: Part3: Bond Convexity Measures Convexity is the measurement of "price curvature" of a bond "in the neighborhood" of the bond's current market rate and price point: Convexity=2V0(y)2V+V+2V0 whereyYY0Y+=0.50%=Y0y=currentmarketrateofbond=Y0+ycorrespondindtoV=priceofbond@YcorrespondingtoV0=currentpriceofbondcorrespondingtoV+=priceofbond@Y+ correspondind to V - = price of bond @ Y - corresponding to V0= current price of bond corresponding to V+=price of bond @ Y+ Thus the measurement is based on "neighborhood" bond prices of V - and V+ which corresponds to change in neighborhood yields -- Y00.5% - i.e. Y - and Y+ from its current bond market rate Y0. Convex Funds, a bond investment company, underwrote a set of bonds with the following characteristics: Using the above formula and data, calculate this bond's Convexity by calculating and filling in the template: fill in thase. calculate these bond prices PS: leave thom in positive numbers. Use above formula to calculate in space bolow Convexity=$345.4550$7.2800 a) Usina the followina temalate calculate this bonds Macaulay Duration D. b) Using the algebrale formula, calculate this bonds Duration D. Hirt you should get the same arsarer as lal. c) Using the Excel formula, calculote this bonds Macaulay Duration D and Modifled Duration D*. PS: the D answer here should be the same as that in [a] and BD. Metes: number of yoars of maturily of the bond, e.q. 0101/2050 if it is a 30-year bond. - Frequency d Coupon PMTs reler io the number of coupon payments per yes, eg " 2 for semi-amul, ete. - For more into on tivis formula, use Excel's Help and search for "Duration". - If this function is not avallatle on your Excel, run the Setup prog am to install the Anaysis Tool Pock. Aher you install the Analysis Tooi Pack, you must enable it by using the Ads-ins command on the Tools menu. Refer be Excel's Help for detail instruction. - The problem with peting "1/12000" and "1/1/2060" is that it makes its use irfexible when you are using mahrity (in number of years) as one of your perameters. One sciltion is to introduce two cells byour calculation: i1 613/21 Then use bot in the parancters of the above Excel formula. - PS: Use "Mduration" with same perameters for calloulatina Modfod Duration D*. Nocik Using Excel formula "DURATION", D = \& use Bacl formula and its porameters to get the D value Usina Excel formula "MDURATION", D*" t use Exal formulo and its porameters to get the 0 value Continuing from previous question, use Modified Duration and Convexity to approximate the percentage change in price of the bond when its market rate change from 5% to 6%. PS; to save time, calculated for you, use a Macaulay Duration D of 15.8407. a) The "first order approximation" of \% BondPrice is a linear approximation. it uses Modified Duration in the following manner: Modified Duration D=1+C/YMktRateMacaulayDurationD Use the following template to fill in and calculate the following data: %BBondPrice%BBondPrice=Dyield=fillinnumbersbyshowingwork=eanswers The "second order approximation" of \% BondPrice is to incorporate the bond"s Convexity measurement: %BondPriceDyield+ConvexityAdjustment Use the following template to calculate and fill in the following data: From previous question's V0, current bond price @ MktRate 5%= fill in ... (Niif] Acutal (accurate) bond price when MiktRate changes to 6%= calculate ... [viii] (Iviii) - (vi) + / (i) = Actual (accurate) %B BondPrice = | [ix] Summary data of bond, copy over from previous calculations: Comparing the error in approximation, calculate and fill in the following: Part3: Bond Convexity Measures Convexity is the measurement of "price curvature" of a bond "in the neighborhood" of the bond's current market rate and price point: Convexity=2V0(y)2V+V+2V0 whereyYY0Y+=0.50%=Y0y=currentmarketrateofbond=Y0+ycorrespondindtoV=priceofbond@YcorrespondingtoV0=currentpriceofbondcorrespondingtoV+=priceofbond@Y+ correspondind to V - = price of bond @ Y - corresponding to V0= current price of bond corresponding to V+=price of bond @ Y+ Thus the measurement is based on "neighborhood" bond prices of V - and V+ which corresponds to change in neighborhood yields -- Y00.5% - i.e. Y - and Y+ from its current bond market rate Y0. Convex Funds, a bond investment company, underwrote a set of bonds with the following characteristics: Using the above formula and data, calculate this bond's Convexity by calculating and filling in the template: fill in thase. calculate these bond prices PS: leave thom in positive numbers. Use above formula to calculate in space bolow Convexity=$345.4550$7.2800 a) Usina the followina temalate calculate this bonds Macaulay Duration D. b) Using the algebrale formula, calculate this bonds Duration D. Hirt you should get the same arsarer as lal. c) Using the Excel formula, calculote this bonds Macaulay Duration D and Modifled Duration D*. PS: the D answer here should be the same as that in [a] and BD. Metes: number of yoars of maturily of the bond, e.q. 0101/2050 if it is a 30-year bond. - Frequency d Coupon PMTs reler io the number of coupon payments per yes, eg " 2 for semi-amul, ete. - For more into on tivis formula, use Excel's Help and search for "Duration". - If this function is not avallatle on your Excel, run the Setup prog am to install the Anaysis Tool Pock. Aher you install the Analysis Tooi Pack, you must enable it by using the Ads-ins command on the Tools menu. Refer be Excel's Help for detail instruction. - The problem with peting "1/12000" and "1/1/2060" is that it makes its use irfexible when you are using mahrity (in number of years) as one of your perameters. One sciltion is to introduce two cells byour calculation: i1 613/21 Then use bot in the parancters of the above Excel formula. - PS: Use "Mduration" with same perameters for calloulatina Modfod Duration D*. Nocik Using Excel formula "DURATION", D = \& use Bacl formula and its porameters to get the D value Usina Excel formula "MDURATION", D*" t use Exal formulo and its porameters to get the 0 value