Convection in a pipe with a constant heat flux at the wall Water flows in an insulated pipe with...

Transcribed Image Text:

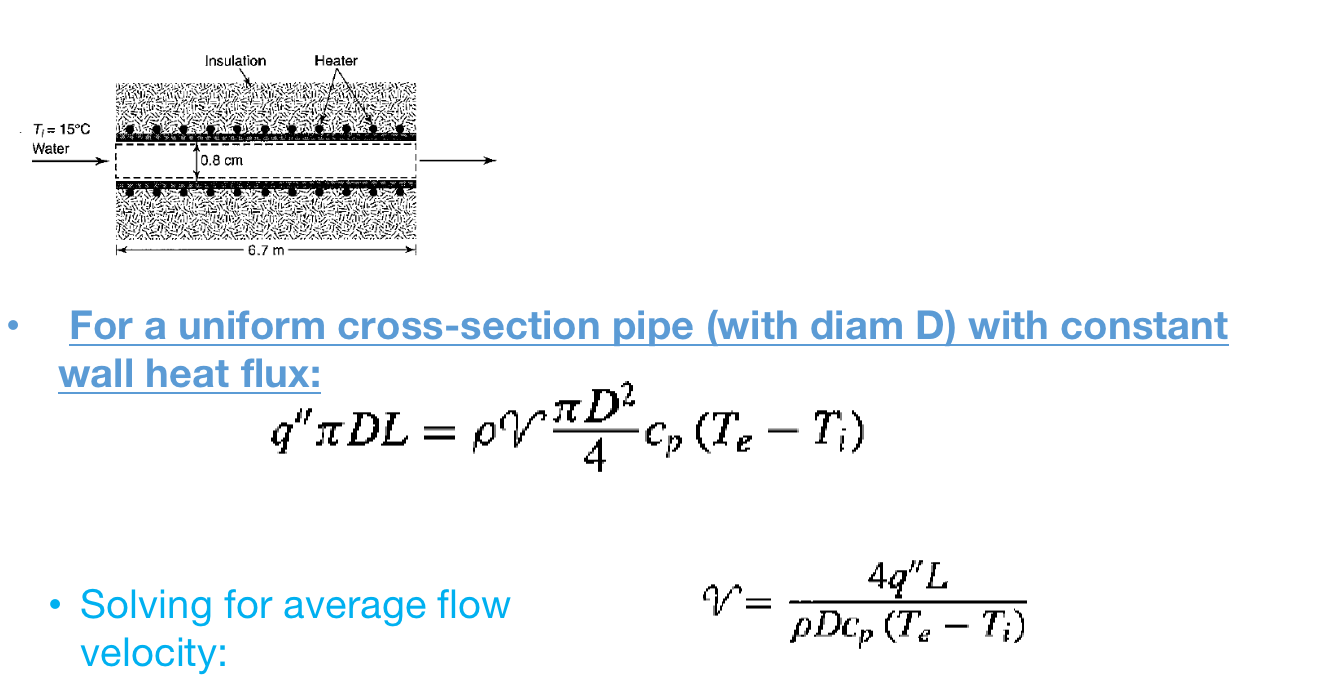
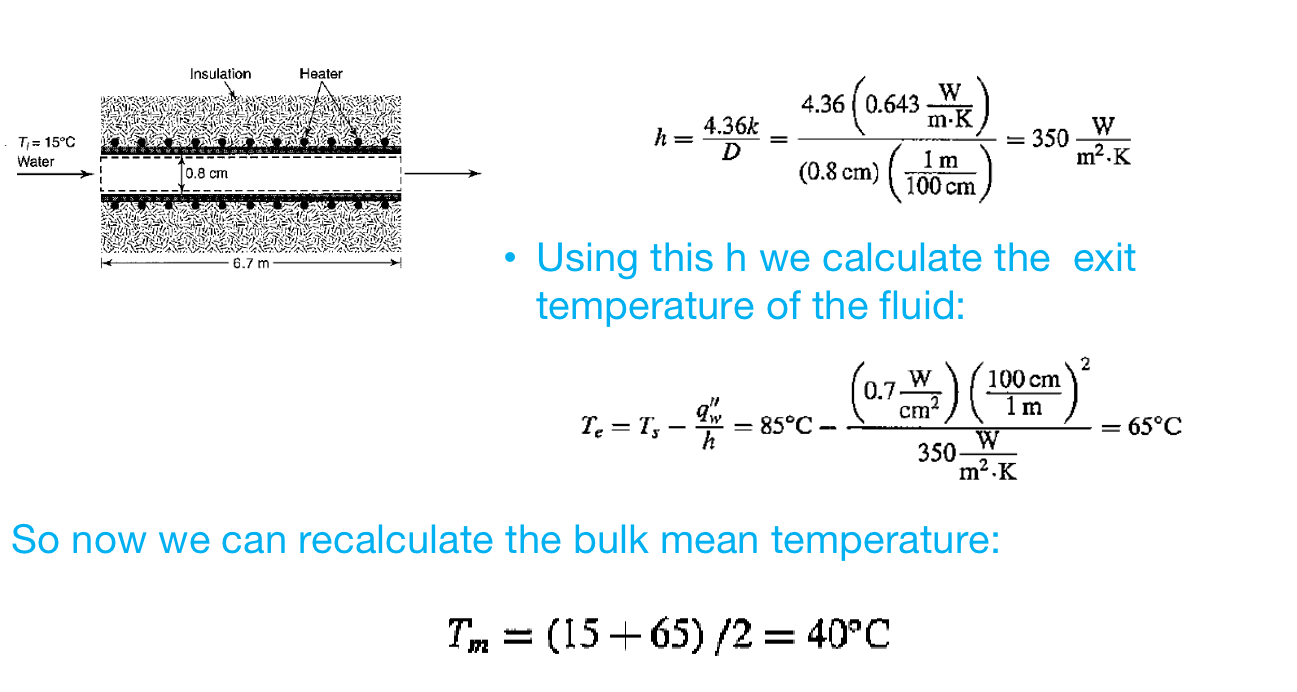
Convection in a pipe with a constant heat flux at the wall Water flows in an insulated pipe with an inside diameter of 0.8 cm and a length of 6.7 m. A constant heat flux of 0.7 W/cm² is applied on the outside wall of the pipe under the insulation. The inlet water temperature is 15°C. If the inside wall temperature must stay below 85°C everywhere along the pipe, what minimum flow velocity is needed? Neglect entrance effects. Insulation Heater = 15°C ter 0.8 cm 6.7 m ● Conservation of energy for the control volume (entire fluid volume in the pipe): Q = mcp (Te - Ti) Total heat transfer rate crossing the boundaries at the fluid-wall interface Total heat transfer rate into the fluid ● T₁= 15°C Water Insulation ● 0.8 cm 6.7 m Heater For a uniform cross-section pipe (with diam D) with constant wall heat flux: q"TDL = p Cp (Te - Ti) - PYTD² 4 Solving for average flow velocity: V= 4q"L pDCp (Te - Ti) • Use relationship we found between the local surface temperature and the local average fluid temperature for the pipe with constant wall heat flux casulation Heater T₁= 15°C Water 0.8 cm 6.7 m ● T₁(x)=T₁(x) qq /h(x) Apply the relationship above at the exit location: • To find h let's guess flow if laminar and fully developed (problem said we can neglect entrance effects so flow is fully developed): Te = Ts NUD Aw h hD k 4.36 T₁= 15°C Water ● Insulation 0.8 cm 6.7 m- Heater ● NUD 4.36 We need properties evaluated at bulk fluid temperature: Tm = (Ti + Te) /2. Because we do not know yet the bulk mean fluid temperature we will need to first guess it: Tm ≈ ½-1 (T; + Ts) ≈ ½ (15 +85) °C = 50°C Next we calculate h with at the guessed average temperature: W m-K h = 4.36k 4.36 0.643 (0.8 cm) hD k Im 100 cm = 350 m².K T₁= 15°C Water Insulation 0.8 cm 6.7 m Heater h = 4.36k D 4.36 (0.643) (0.8 cm) (100cm) T₁=T₁-2 = 85°C- Using this h we calculate the exit temperature of the fluid: = 350 0.7 W) (100 cm W m².K 350- So now we can recalculate the bulk mean temperature: Tm (15+65)/2 = 40°C m².K 2 65°C T₁= 15°C Water Insulation ● Heater 0.8 cm ● Tm ≈ ½-1 (T; +Ts) ≈ ½⁄3 (15 +85) °C = 50°C Difference in values is 10 degrees! Homework: reiterate properties using the last calculation of Te to find Tm for next iteration, h, new Te and new Tm until your last iteration value for Tm is within 1 degree of the previous Tm iteration Tm = (15+65)/2 = 40°C But our first guess was: • Next calculate the average fluid velocity ● using last iteration for Te value: Finally cross-check if Reynolds number is indeed for laminar flow: V= 4q"L pDcp (Te - Ti) Re= pDVm μl

Answer rating: 100% (QA)