Convert this MATLAB code to Java code and run the program.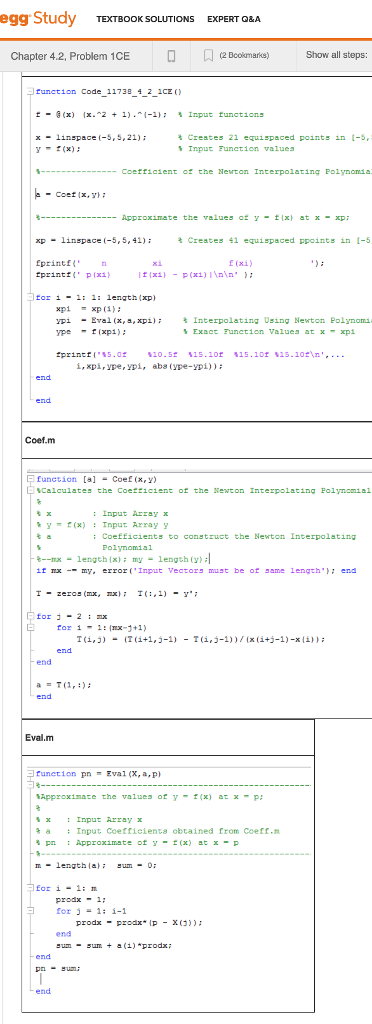

| egg Study TEXTBoOK SOLUTIONS EXPERT O&A Chapter 4.2. Problem ICE ? ? (2Boolmans) Show all steps: unction Code 11738_4_2 iCE ) f-g(x) {x."2 + 1)."(-1); x-linspace(-5,5,21); Input functions Creates 21 equispaced points in -5 % Input Function value Coefficient of the Newton Interpolating Polynomia " coef (x, y); ?-???? Approximate xplinspace(-5,5,41) Eprintf the values of y-f(x) at x-xp; xi E (xi) printt' pxi or i-1: 1: length (xp) xpi xp () Pi-Eval (x, s, xpi) Interpolating Using Newton Polynomi Exa Function value, at x-xpi i,xpirype,ypi, aba (ype-ypi)) end Coef.m function [a] -Coef(x,Y) Calculates the Coefficient of the Newton Interpolating Polynomial Input Arrayx f (x) Input Array y y Coefficients to construct the Newton Interpolating Polynomiai %--nx-length(x); my-length (y) ; If mx-" my, error ('Input vectors must be of ame length" }; end for j-2;mx or 11: x-3+1) end Eval.m tunction pn Eval (X, a,p) Approxinace the values of y x) atxP x : Input Array x ?a ; Input coefficients trom Coeff.m pn : Approximate of y-f(x) at x-p or i1: m prodx1 for j-1: i-1 end -end end | egg Study TEXTBoOK SOLUTIONS EXPERT O&A Chapter 4.2. Problem ICE ? ? (2Boolmans) Show all steps: unction Code 11738_4_2 iCE ) f-g(x) {x."2 + 1)."(-1); x-linspace(-5,5,21); Input functions Creates 21 equispaced points in -5 % Input Function value Coefficient of the Newton Interpolating Polynomia " coef (x, y); ?-???? Approximate xplinspace(-5,5,41) Eprintf the values of y-f(x) at x-xp; xi E (xi) printt' pxi or i-1: 1: length (xp) xpi xp () Pi-Eval (x, s, xpi) Interpolating Using Newton Polynomi Exa Function value, at x-xpi i,xpirype,ypi, aba (ype-ypi)) end Coef.m function [a] -Coef(x,Y) Calculates the Coefficient of the Newton Interpolating Polynomial Input Arrayx f (x) Input Array y y Coefficients to construct the Newton Interpolating Polynomiai %--nx-length(x); my-length (y) ; If mx-" my, error ('Input vectors must be of ame length" }; end for j-2;mx or 11: x-3+1) end Eval.m tunction pn Eval (X, a,p) Approxinace the values of y x) atxP x : Input Array x ?a ; Input coefficients trom Coeff.m pn : Approximate of y-f(x) at x-p or i1: m prodx1 for j-1: i-1 end -end end