Could you please work out the blank sections of the questions, i am completely lost and dont even know where to begin with them
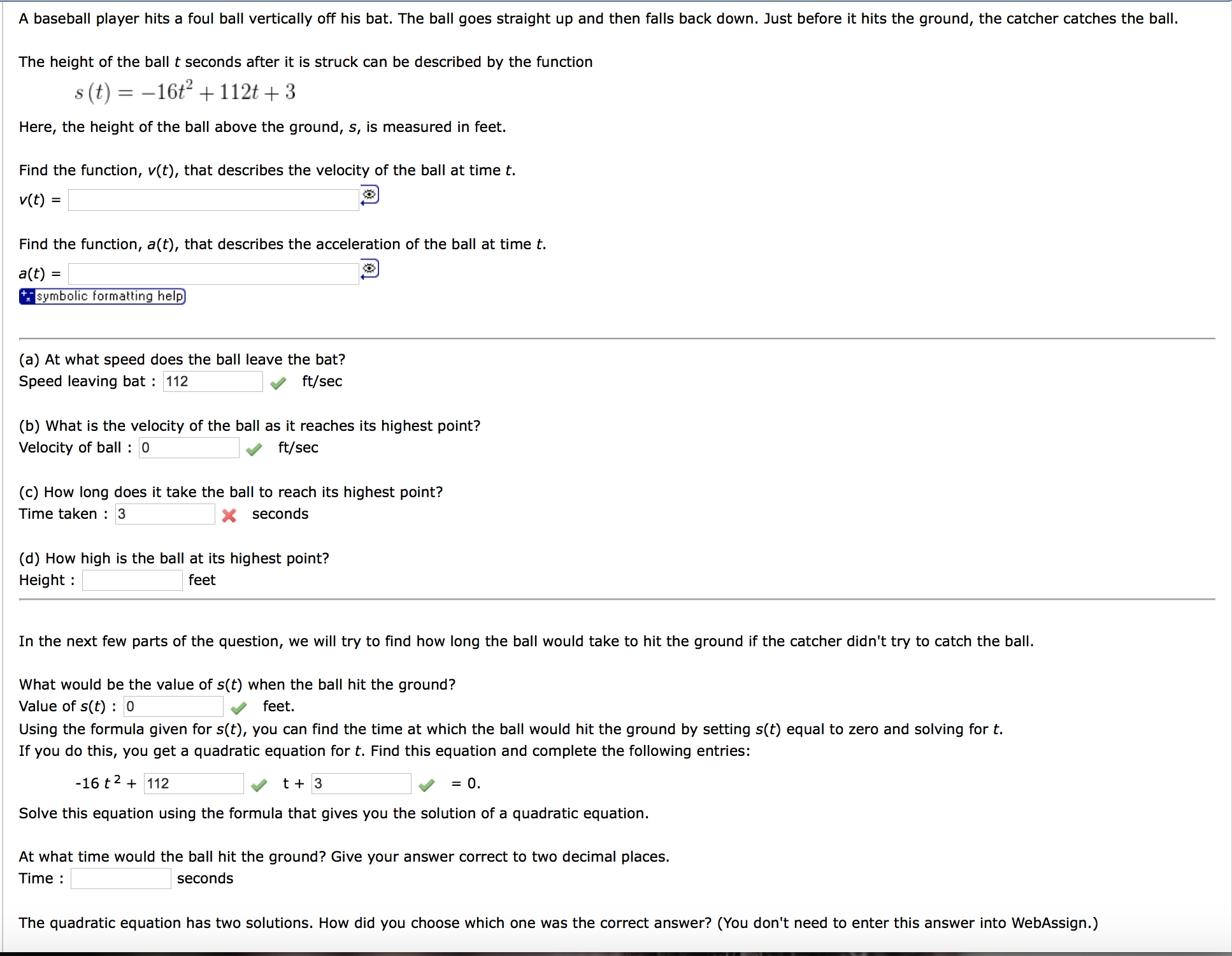
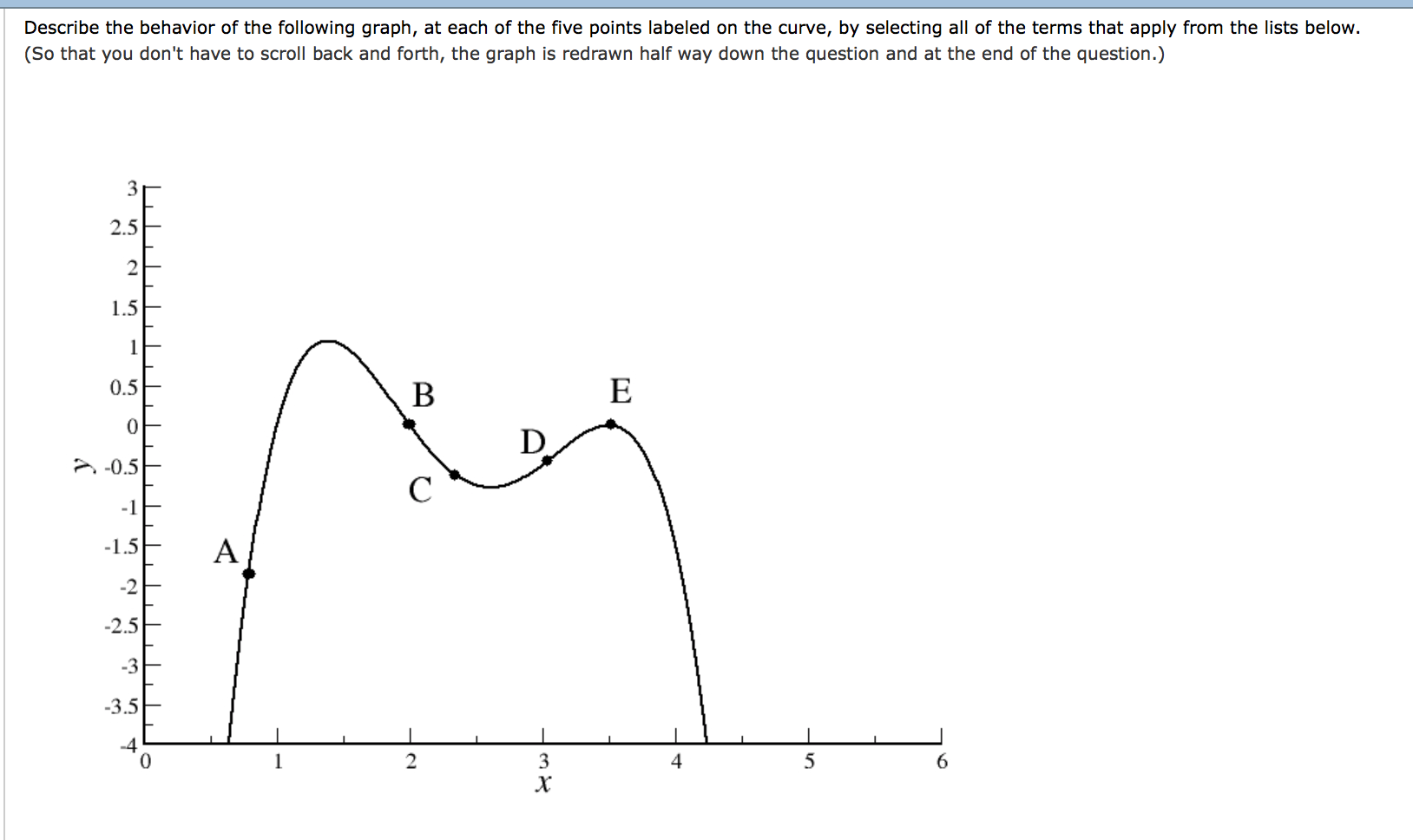
A baseball player hits a foul ball vertically off his bat. The ball goes straight up and then falls back down. Just before it hits the ground, the catcher catches the ball. The height of the ball t seconds after it is struck can be described by the function s(t) = 16t2 +112t+ 3 Here, the height of the ball above the ground, 5, is measured in feet. Find the function, v(t), that describes the velocity of the ball at time t. v(t) = @ Find the function, a(t), that describes the acceleration of the ball at time t. a(t) = @ *J symbolic lotmalting help (a) At what speed does the ball leave the bat? Speed leaving bat : 112 ft/sec (b) What is the velocity of the ball as it reaches its highest point? Velocity of ball : 0 J ft/sec (c) How long does it take the ball to reach its highest point? Time taken : x seconds (d) How high is the ball at its highest point? Height : feet In the next few parts of the question, we will try to nd how long the ball would take to hit the ground if the catcher didn't try to catch the ball. What would be the value of s(r) when the ball hit the ground? Value of 503) : 0 feet. Using the formula given for s(t), you can find the time at which the ball would hit the ground by setting 50:) equal to zero and solving for t. If you do this, you get a quadratic equation for t. Find this equation and complete the following entries: -16t2+112 q t+3 ,I =0. Solve this equation using the formula that gives you the solution of a quadratic equation. At what time would the ball hit the ground? Give your answer correct to two decimal places. Time : seconds The quadratic equation has two solutions. How did you choose which one was the correct answer? (You don't need to enter this answer into WebAssign.) # Describe the behavior of the following graph, at each of the ve points labeled on the curve, by selecting all of the terms that apply from the lists below. (50 that you don't have to scroll back and forth, the graph is redrawn half way down the question and at the end of the question.) Point B for) is increasing for) is decreasing the slope of for) is increasing the slope of f(x) is decreasing for) has a relative minimum for) has a relative maximum x) has an inflection point for) is concave upwards x) is concave downwards Point C x) is increasing x) is decreasing the slope of x) is increasing the slope of x) is decreasing x) has a relative minimum x) has a relative maximum x) has an inflection point x) is concave upwards x) is concave downwards Point D x) is increasing x) is decreasing the slope of x) is increasing the slope of x) is decreasing x) has a relative minimum x) has a relative maximum x) has an inflection point x) is concave upwards x) is concave downwards