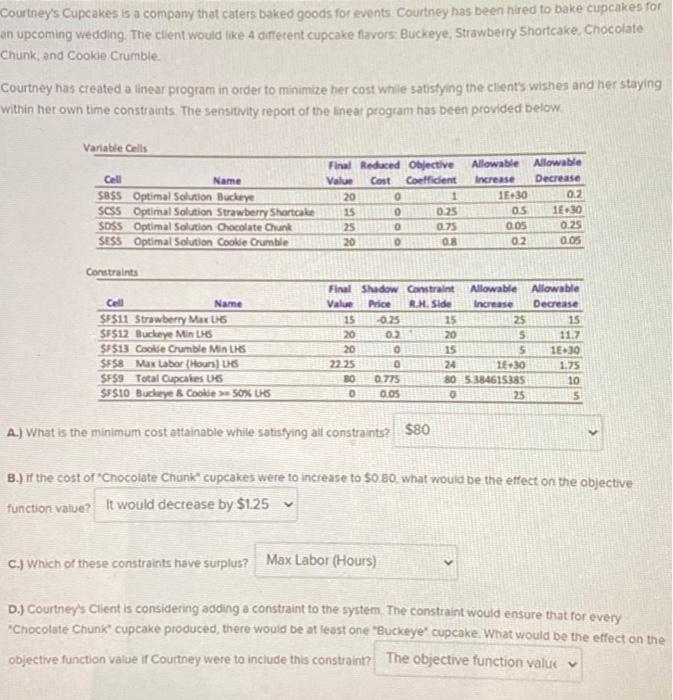
Courtney's Cupcakes is a company that caters baked goods for events Courtney has been hired to bake cupcakes for an upcoming wedding. The client would like 4 different cupcake flavors: Buckeye, Strawberry Shortcake Chocolate Chunk, and Cookie Crumble. Courtney has created a linear program in order to minimize her cost while satistying the client's wishes and her staying within her own time constraints. The sensitivity report of the lineat program has been provided below. Variable Cells Cell Name SBSS Optimal Solution Buckeye SCSS Optimal Solution Strawberry Shortcake SOSS Optimal Solution Chocolate Chunk SESS Optimal Solution Cookie Crumble Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 20 1 15.30 0.2 15 0 0.25 OS 15.30 25 0 0.75 COS 0.25 20 0 08 02 0.05 Constraints Cell Name $F$11 Strawberry Max LH6 $F$12 Buckeye Min HS $F513 Cookie Crumble Mints $858 Max Labor (Hours) 1166 SF59 Total Cupcakes US SF510 Buckeye 8 Cookie > 50% LHS Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 15 -0.25 15 25 15 20 02 20 5 11.7 20 0 15 5 1E30 22 25 24 1.30 1.75 30 0.775 80 5.384615385 10 O 0.05 0 25 5 A.) What is the minimum cost attainable while satisfying at constraints? $80 B.) it the cost of Chocolate Chunk cupcakes were to increase to $0 80 what would be the effect on the objective function value? It would decrease by $1.25 C.) Which of these constraints have surplus? Max Labor (Hours) D.) Courtney's Client is considering adding a constraint to the system. The constraint would ensure that for every Chocolate Chunk cupcake produced there would be at least one "Buckeye' cupcake. What would be the effect on the objective function value if Courtney were to include this constraint? The objective function value v Courtney's Cupcakes is a company that caters baked goods for events Courtney has been hired to bake cupcakes for an upcoming wedding. The client would like 4 different cupcake flavors: Buckeye, Strawberry Shortcake Chocolate Chunk, and Cookie Crumble. Courtney has created a linear program in order to minimize her cost while satistying the client's wishes and her staying within her own time constraints. The sensitivity report of the lineat program has been provided below. Variable Cells Cell Name SBSS Optimal Solution Buckeye SCSS Optimal Solution Strawberry Shortcake SOSS Optimal Solution Chocolate Chunk SESS Optimal Solution Cookie Crumble Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 20 1 15.30 0.2 15 0 0.25 OS 15.30 25 0 0.75 COS 0.25 20 0 08 02 0.05 Constraints Cell Name $F$11 Strawberry Max LH6 $F$12 Buckeye Min HS $F513 Cookie Crumble Mints $858 Max Labor (Hours) 1166 SF59 Total Cupcakes US SF510 Buckeye 8 Cookie > 50% LHS Final Shadow Constraint Allowable Allowable Value Price R.H. Side Increase Decrease 15 -0.25 15 25 15 20 02 20 5 11.7 20 0 15 5 1E30 22 25 24 1.30 1.75 30 0.775 80 5.384615385 10 O 0.05 0 25 5 A.) What is the minimum cost attainable while satisfying at constraints? $80 B.) it the cost of Chocolate Chunk cupcakes were to increase to $0 80 what would be the effect on the objective function value? It would decrease by $1.25 C.) Which of these constraints have surplus? Max Labor (Hours) D.) Courtney's Client is considering adding a constraint to the system. The constraint would ensure that for every Chocolate Chunk cupcake produced there would be at least one "Buckeye' cupcake. What would be the effect on the objective function value if Courtney were to include this constraint? The objective function value v