Create a complete binary tree;

a. Choose the most efficient data structure to implement the nave sort algorithm. Justify your choice b. Write a function named naiveSort() that receives the original list, and then sorts it in ascending order using the algorithm described in above 4 steps (naiveSort.cpp). c. Calculate the time complexity of naiveSort() function (answers.pdf). d. Calculate the space complexity of naiveSort() function (answers.pdf).

For clarification, the GIVEN functions:

Creating Tree: [for example, ceil(2.3) is 3]. Therefore, the number of leaves in the tree is always equal or more than n. Now, store all the elements of the array in the first n leaves of highest level of tree from left to right. Store a value (E) greater than any element in the array for every empty leaf; for example, you can use INT_MAX of climits library as the value of an empty leaf. The following tree shows an example where Data={8, 20, 0, 7, 2}, h=ceil(log2(5))+1=4 and E=INT_MAX.

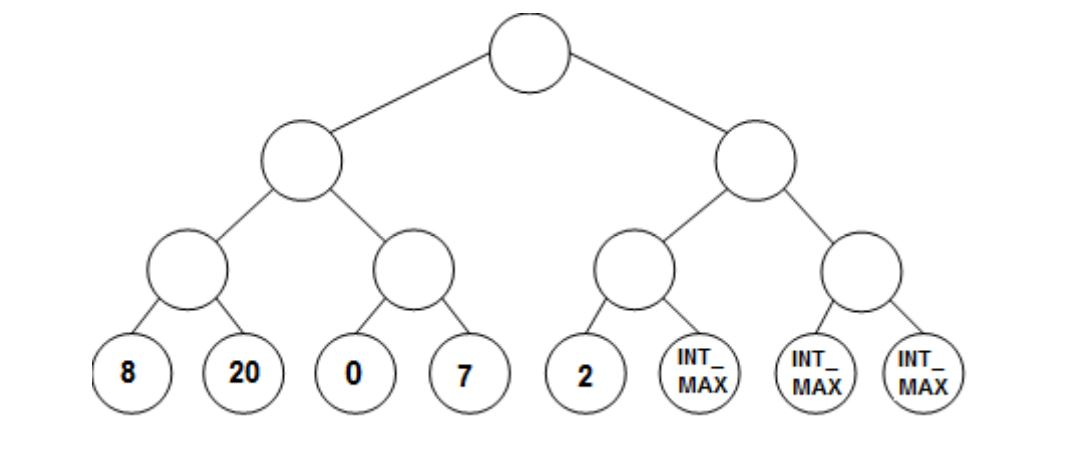Populating Tree: As you can see in the above tree, all the internal nods have no value. To populate and initialize the internal nodes of tree, start from the bottom of the tree, and assign each internal node with the minimum value of its two children, as shown in the following tree. This ensures to assign the smallest value in the list, min, to the root. You must then store this minimum value in its right place in the original list, ie. data. After this step, the first item of data is updated like: data={0, 20, 0, 7, 2}. Note that valid elements in the original list are shown in red.

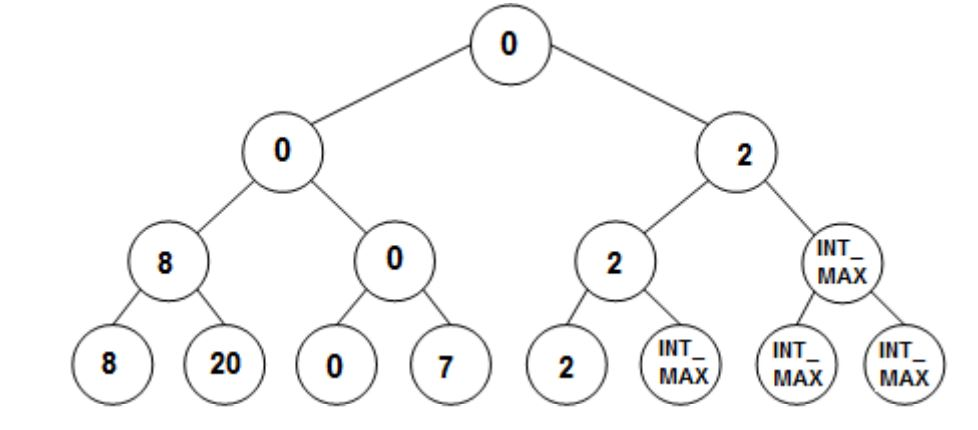
. Finding Next Minimum: First stores E (or INT_MAX) in the leaf that contains min value (is shown in following tree). Then starting from the bottom and assign each internal nodes to the minimum of its two children. Again the root carries the next minimum value of the original list, ie: data= {0, 2, 0, 7, 2}. The following figure displays the tree after one iteration of finding the next minimum value.

Sorting Data: repeat step 3 until the root becomes E (or INT_MAX). The following tree shows another iteration of the algorithm (finding next minimum is considered as an iteration), and data is updated to {0, 2, 7, 7, 2}.

INT MAX INT MAX INT MAX INT MAX INT INT MAX INT MAX MAX INT MAX INT MAX INT MAX INT MAX INT INT MAX INT MAX MAX