(Cryptography: An interactive protocol for discrete log)

Setup: p is a large prime, g is a primitive element of Z_p , and b = g^a mod p. Each of p, g, and b is public, but a is private to Pat.

Pat claims: He knows a (i.e., dlog_g(b)).

Repeat n-many times: Pat chooses r Z_p1,randomly , computes h₁ = g^r mod p and h₂ = g^ar mod p and sends (h₁, h₂) to Vanna.

Vanna chooses i { 1, 2 }, randomly. If i = 1, then she ask Pat to send her r₁ = r. If i = 2, then she ask Pat to send her r₂ = a r.

Vanna, after receiving r_i , checks that h₁ h₂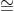 b (mod p) and h_i 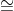g^r_i (mod p) If either fails, she rejects.

If Vanna has not rejected after n-many rounds, she accepts.

(a) Prove that the above is complete.

(b) Prove that the above is sound.

Reference

|A| = the number of elements in set A.

(n) = |{ a Z⁺_n : gcd(a, n) = 1 }|.

Eulers Theorem: For each n > 1 and a Z_n : a⁽ⁿ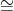⁾ 1 (mod n).

g is a primitive element of Z_n iff { g¹ , g² , . . . , g⁽ⁿ⁾ } = Z_n .

Suppose g is a primitive element of Z_n . For a Z_n, the discrete log of a to the base g mod p (written: dlog_g (a)) is the solution for x of: g^x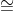 a (mod n), i.e., g ^dlog_g(a) 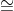a (mod n).

Definition. Suppose a, n Z with n > 1 and a 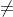0. (a) a is a quadratic residue mod n when x² a (mod n) has a solution, otherwise a is a nonresidue. (b) QR_n = the quadratic residues mod n. (c) Suppose n is the product of two distinct odd primes p and q. 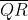n = { a : ( ) = 1 = ( ) } = the pseudo-residues mod n.