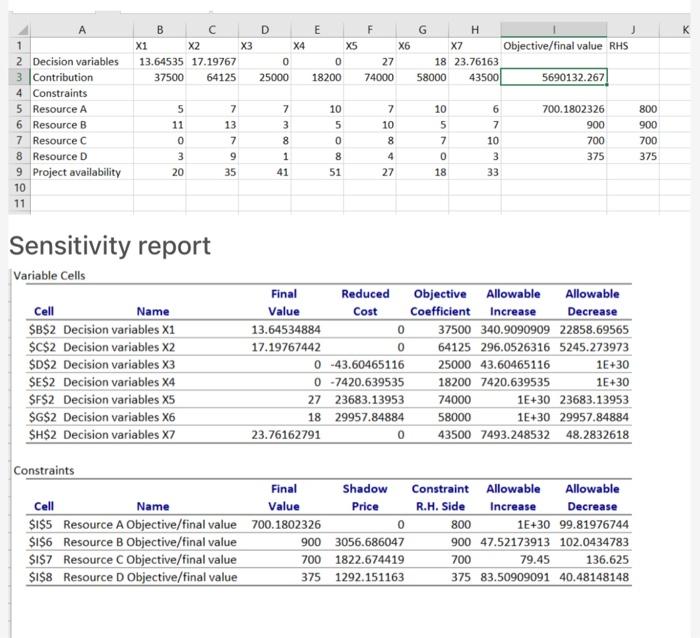
D E F K X1 X2 X3 13.64535 17.19767 37500 64125 X4 0 X5 0 X6 27 74000 GH X7 Objective/final value RHS 18 23.76163 58000 43500 5690132.267 25000 18200 7 10 1 2 Decision variables 3 Contribution 4 Constraints 5 Resource A 6 Resource B 7 Resource 8 Resource D 9 Project availability 10 11 10 5 11 0 3 7 13 7 9 35 7 3 8 1 41 10 5 0 8 51 700.1802326 900 700 375 6 7 10 3 33 800 900 700 375 8 4 27 7 0 18 20 Sensitivity report Variable Cells Cell Name $B$2 Decision variables X1 $C$2 Decision variables X2 $D$2 Decision variables X3 $E$2 Decision variables X4 $F$2 Decision variables X5 $G$2 Decision variables X6 $H$2 Decision variables X7 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 13.64534884 0 37500 340.9090909 22858.69565 17.19767442 0 64125 296.0526316 5245.273973 0-43.60465116 25000 43.60465116 1E+30 0-7420.639535 18200 7420.639535 1E+30 27 23683.13953 74000 1E+30 23683.13953 18 29957.84884 58000 1E+30 29957.84884 23.76162791 0 43500 7493.248532 48.2832618 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $I$5 Resource A Objective/final value 700.1802326 0 800 1E+30 99.81976744 $I$6 Resource B Objective/final value 900 3056.686047 900 47.52173913 102.0434783 $1$7 Resource C Objective/final value 700 1822.674419 700 79.45 136.625 $I$8 Resource D Objective/final value 375 1292.151163 375 83.50909091 40.48148148 d). There may be a Reduced Cost in your Sensitivity Report that has a value for a variable that is O in the optimal solution? If so, what change(s) in the objective function coefficient will make that variable(s) profitable? What is the new value of the objective function coefficient? 12 13 14 15 16 17 18 19 20 21 22 23 24 e). Use the parameters function in the Analytic Solver Platform to vary the value # Prits Available for the Project Type 7. Set the lower limit of the values to 50% of the Base, and set the upper limit to 150% of the base. Show how the value of the Objective Function is affected by these changes. f). Since the problem is about choosing projects, the selection of a partial project is problematic. If your solution contains partial projects, add an additional Integer constraint for each decision variable that contains a fraction. (This is available in the constraint building area of Solver). How does this change your solution--what is the new Objective Function value? Can you make a general statement about what will happen when a continuous variable solution is forced to be integer? D E F K X1 X2 X3 13.64535 17.19767 37500 64125 X4 0 X5 0 X6 27 74000 GH X7 Objective/final value RHS 18 23.76163 58000 43500 5690132.267 25000 18200 7 10 1 2 Decision variables 3 Contribution 4 Constraints 5 Resource A 6 Resource B 7 Resource 8 Resource D 9 Project availability 10 11 10 5 11 0 3 7 13 7 9 35 7 3 8 1 41 10 5 0 8 51 700.1802326 900 700 375 6 7 10 3 33 800 900 700 375 8 4 27 7 0 18 20 Sensitivity report Variable Cells Cell Name $B$2 Decision variables X1 $C$2 Decision variables X2 $D$2 Decision variables X3 $E$2 Decision variables X4 $F$2 Decision variables X5 $G$2 Decision variables X6 $H$2 Decision variables X7 Final Reduced Objective Allowable Allowable Value Cost Coefficient Increase Decrease 13.64534884 0 37500 340.9090909 22858.69565 17.19767442 0 64125 296.0526316 5245.273973 0-43.60465116 25000 43.60465116 1E+30 0-7420.639535 18200 7420.639535 1E+30 27 23683.13953 74000 1E+30 23683.13953 18 29957.84884 58000 1E+30 29957.84884 23.76162791 0 43500 7493.248532 48.2832618 Constraints Final Shadow Constraint Allowable Allowable Cell Name Value Price R.H. Side Increase Decrease $I$5 Resource A Objective/final value 700.1802326 0 800 1E+30 99.81976744 $I$6 Resource B Objective/final value 900 3056.686047 900 47.52173913 102.0434783 $1$7 Resource C Objective/final value 700 1822.674419 700 79.45 136.625 $I$8 Resource D Objective/final value 375 1292.151163 375 83.50909091 40.48148148 d). There may be a Reduced Cost in your Sensitivity Report that has a value for a variable that is O in the optimal solution? If so, what change(s) in the objective function coefficient will make that variable(s) profitable? What is the new value of the objective function coefficient? 12 13 14 15 16 17 18 19 20 21 22 23 24 e). Use the parameters function in the Analytic Solver Platform to vary the value # Prits Available for the Project Type 7. Set the lower limit of the values to 50% of the Base, and set the upper limit to 150% of the base. Show how the value of the Objective Function is affected by these changes. f). Since the problem is about choosing projects, the selection of a partial project is problematic. If your solution contains partial projects, add an additional Integer constraint for each decision variable that contains a fraction. (This is available in the constraint building area of Solver). How does this change your solution--what is the new Objective Function value? Can you make a general statement about what will happen when a continuous variable solution is forced to be integer