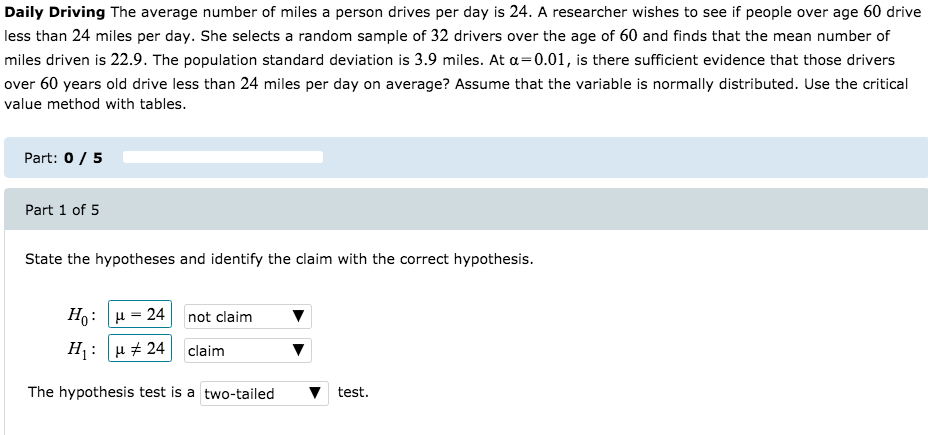
Daily Driving The average number of miles a person drives per day is 24. A researcher wishes to see if people over age 60 drive less than 24 miles per day. She selects a random sample of 32 drivers over the age of 60 and finds that the mean number of miles driven is 22.9. The population standard deviation is 3.9 miles. At a=0.01, is there sufficient evidence that those drivers over 60 years old drive less than 24 miles per day on average? Assume that the variable is normally distributed. Use the critical value method with tables. Part: 0 / 5 Part 1 of 5 State the hypotheses and identify the claim with the correct hypothesis. Ho LL = 24 not claim HE H # 24 claim The hypothesis test is a two-tailed test.Find the critical value(s). Round the answer to at least two decimal places. If there is more than one critical value, separate them with commas. Critical value(s): D Compute the best value. Always round z score values to at least two decimal places. =m Make the decision. Reject the null hypothesis. Part: 4 / 5 Part 5 of 5 not enough evidence to support the claim enough evidence to support the claim Summari enough evidence to reject the claim not enough evidence to reject the claim There is (Choose one) that drivers over 60 years old drive less than 24 miles per day, on average.[cl] Make the decision. Do not reject T the null hypothesis. (e) Summarize the results. There [Choose one} 1' enough evidence to support the claim that the average calorie content is greater than ll. (b) Find the critical value(s). Round the answer to three decimal places, if necessary. If there is more than one critical value, separate them with commas. Critical value(s) : Part: 2 / 5 Part 3 of 5 (c) Compute the test value. Round the sample statistics to one decimal place and t score value to at least three decimal places. t =Chocolate Chip Cookie Calories The average 1-ounce chocolate chip cookie contains 110 calories. A random sample of 15 different brands of 1-ounce chocolate chip cookies resulted in the following calorie amounts. At the a=0.01 level, is there sufficient evidence that the average calorie content is greater than 110 calories? Assume the population is normally distributed. 105 100 185 100 115 110 150 120 180 120 151 100 130 152 140 Send data to Excel Part 1 of 5 (a) State the hypotheses and identify the claim. Ho: 4 = 110 not claim H1 : H > 110 claim This hypothesis test is a one-tailed test