Data Structure C++

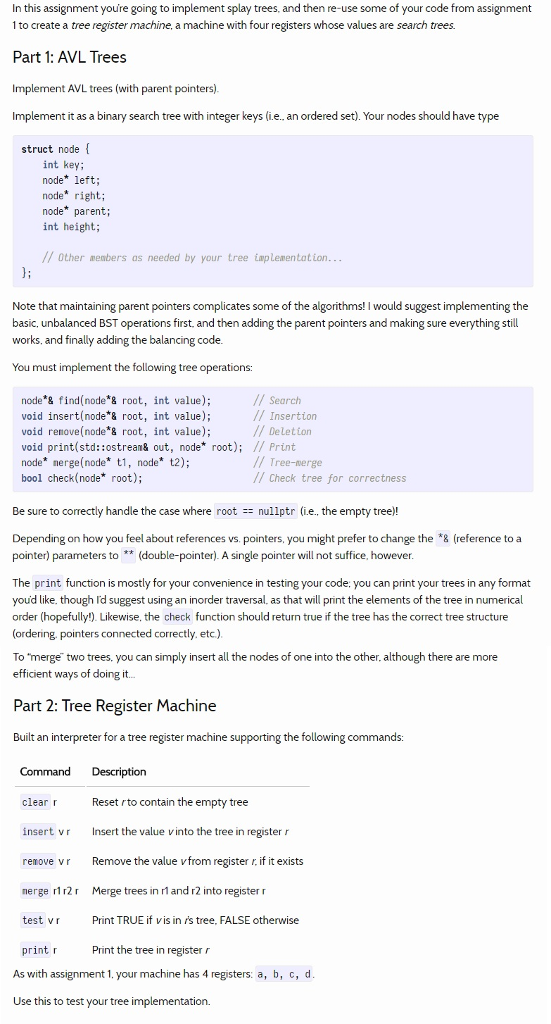
In this assignment you're going to implement splay trees, and then re-use some of your code from assignment 1 to create a tree register machine, a machine with four registers whose values are search trees. AVL Trees Implement AVL trees (with parent pointers). Implement it as a binary search tree with integer keys (i.e., an ordered set). Your nodes should have type struct node {int key; node* left; node* right; node* parent; int height;//Other as needed by your tree implementation...}; Note that maintaining parent pointers complicates some of the algorithms! I would suggest implementing the basic, unbalanced BST operations first, and then adding the parent pointers and making sure everything still works, and finally adding the balancing code. You must implement the following tree operations: node*& find(node*& root, int value);//Search void insert(node*& root, int value);//Insertion void remove(node*& root, int value);//Deletion void print(std::ostream& out, node* root);//Print node* merge(node* t1, node* t2);//Tree-merge bool check(node* root);//Check tree for correctness Be sure to correctly handle the case where root == nullptr (i.e., the empty tree)! Depending on how you feel about references vs. pointers, you might prefer to change the *g (reference to a pointer) parameters to ** (double-pointer). A single pointer will not suffice, however. The print function is mostly for your convenience in testing your code; you can print your trees in any format you'd like, though I'd suggest using an inorder traversal, as that will print the elements of the tree in numerical order (hopefully!). Likewise, the check function should return true if the tree has the correct tree structure (ordering, pointers connected correctly, etc) To "merge" two trees, you can simply insert all the nodes of one into the other, although there are more efficient ways of doing it... Tree Register Machine Built an interpreter for a tree register machine supporting the following commands: As with assignment 1, your machine has 4 registers: a, b, c, d. Use this to test your tree implementation