Day 5 - Linear Regression

Is one's political affiliation likely to influence one's support for same-sex marriage?

To answer our question, we conducted a survey of citizens in five U.S. states, to determine the percentage of adults who voted Democrat in the last election, and the percentage of adults who support the legalization of same-sex marriage.

After compiling our results, we discovered the following:

U.S. State Democratic Vote Same-Sex Support 20%

Alabama 30% 20%

Georgia 35% 30%

Wyoming 40% 40%

Ohio 50% 60%

New York 65% 90 %

1. (a)From this data,extrapolatethe support of same-sex marriage among citizens in Texas (25% Democrats) and in California (60% Democrats). Explain how you arrived at your results.
2. (b)Determine an equation for thelinear regression line. It will be of this form Marriage Support Rate =Democrat Rate?.
3. (c)From the above equation (or from the above data), extrapolate the support of same-sex marriage among citizens in Utah (15% Democrats) and in Massachusetts (75% Democrats).
4. What goes wrong?
5. (d)Let?xand?xbe (respectively) the mean and standard deviation of the Democratic vote. Sim- ilarly, let?yand?ybe the mean and standard deviation of the Same-Sex Support Rate.
6. We can show that?x=30+35+40+50+65= 445
7. and?x=?(44?30)2+(44?35)2+(44?40)2+(44?50)2+(44?65)2= 13.87444.5?1
8. Now run a similar calculation to determine the values of?yand?y.

Aregression linesummarizes the relationship between two variables, but only in a specific setting: when theexplanatoryvariablexhelps explain or predict theresponsevariabley.

There are many types of regression lines, but the one we will use is theleast-squaresregression line: this is the line that "comes closest" to passing through all of the points on ourscatterplot. More specifically, it is the line that makes the sum of the squares of the vertical distances of the data points from the line as small as possible.

Ifxis our explanatory variable, andyis our response variable, then the equation of the least- squares regression line is:

y=mx+b,withslopem=r?yandinterceptb=?y?m?x,?x

whereris thecorrelation coefficientof variablesxandy. And as we had before,?xand?yare the means ofxandy, and?xand?yare the standard deviations ofxandy.

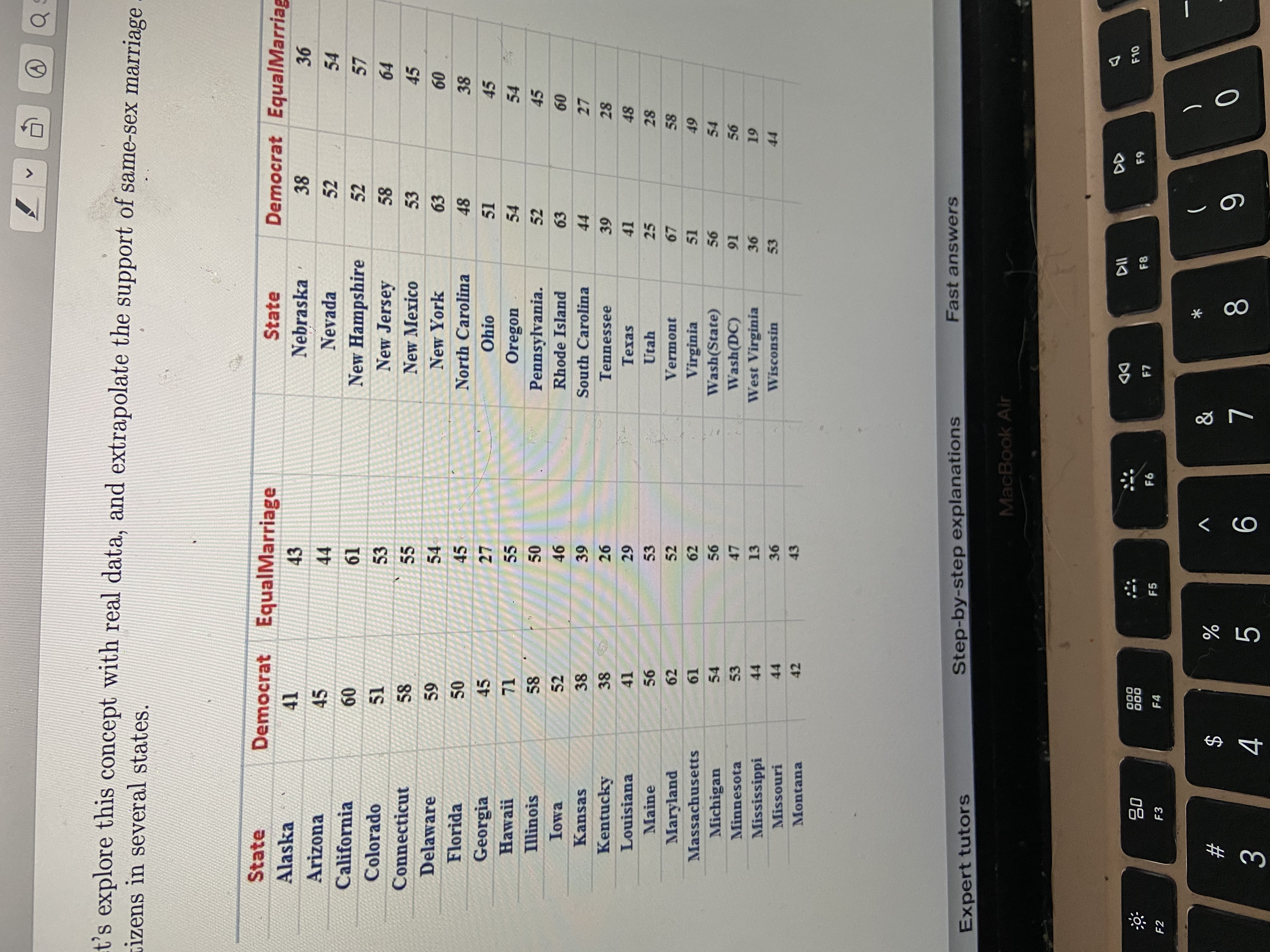
Let's explore this concept with real data, and extrapolate the support of same-sex marriage among citizens in several states.

A Q t's explore this concept with real data, and extrapolate the support of same-sex marriage cizens in several states. State Democrat EqualMarriage State Democrat EqualMarriage Alaska 41 43 Nebraska 38 36 Arizona 45 44 Nevada 52 54 California 60 61 New Hampshire 52 57 Colorado 51 53 New Jersey 58 64 53 45 Connecticut 58 55 New Mexico 60 Delaware 59 54 New York 63 Florida 50 North Carolina 48 38 Georgia 45 Ohio 51 45 54 54 Hawaii 71 Oregon 52 45 Illinois 58 Pennsylvania. 63 60 Iowa 52 Rhode Island 27 Kansas 38 South Carolina 44 Tennessee 39 28 Kentucky 38 26 48 Louisiana 41 29 Texas 41 Utah 25 28 Maine 56 Vermont 67 58 Maryland 62 51 Massachusetts 61 Virginia 49 Wash(State) 56 54 Michigan 54 Wash(DC) 91 56 Minnesota 53 West Virginia 36 19 Mississippi 44 Wisconsin 53 Missouri 44 42 Montana Step-by-step explanations Fast answers Expert tutors MacBook Air DD A DII F9 F10 80 898 F8 F5 F6 F7 F3 F4 & $ % O # 8 4 5 6