def generate_values():

import numpy as np

from sklearn.datasets import make_classification

##########################################

# Generate Naive Bayes Data

##########################################

np.random.seed(6)

X1 = np.random.choice([0,1], size=(100_000,10), p=[0.8, 0.2])

betas = np.random.uniform(0, 1, size=10)

z = X1 @ betas - 1

p = 1 / (1 + np.exp(-z))

y1 = np.where(p

Nspam = 462 + 500

Nham = 10000 - Nspam

s0 = np.argwhere(y1 == 0)[:Nham].flatten()

s1 = np.argwhere(y1 == 1)[:Nspam].flatten()

sel = np.hstack([s0,s1])

sel = np.random.choice(sel, size=10_000, replace=False)

X1 = X1[sel, :]

y1 = y1[sel]

##########################################

# Generate Logistic Regression Data

##########################################

X2, y2 = make_classification(n_samples=1000, n_features=4, n_informative=4, n_redundant=0, n_classes=2, random_state=7)

return X1, y1, X2.round(3), y2

def unit_test_1(add_ones):

import numpy as np

global X2

try:

XE = add_ones(X2)

except:

print('Function results in an error.')

return

if not isinstance(XE, np.ndarray):

print(f'Returned object is not an array. It has type {type(XE)}.')

return

if XE.shape != (1000, 5):

print('Shape of returned array is not correct.')

return

if (XE[:,0] == 1).sum() != 1000:

print('First column does not consist entirely of ones.')

return

if np.sum(XE[:,1:] == X2) != 4000:

print('Returned array does not contain copy of feature array.')

return

print('All tests passed.')

def unit_test_2(predict_proba):

import numpy as np

global X2

betas1 = [2, -1, -3, 2, 3]

betas2 = [5, 1, -4, 3, 5]

try:

p1 = predict_proba(X2, betas1)

p2 = predict_proba(X2, betas2)

except:

print('Function results in an error.')

return

if not isinstance(p1, np.ndarray):

print(f'Returned object is not an array. It has type {type(p1)}.')

return

if p1.shape != (1000,):

print('Shape of returned array is not correct.')

return

check1 = list(p1[:5].round(4)) == [0.2505, 0.996, 0.027, 0.0046, 0.1021]

check2 = list(p2[:5].round(4)) == [0.0166, 0.9998, 0.9388, 0.0009, 0.662]

if not (check1 and check2):

print('Probability estimates are incorrect.')

return

print('All tests passed.')

def unit_test_3(calculate_NLL):

import numpy as np

global X2, y2

betas1 = [2, -1, -3, 2, 3]

betas2 = [5, 1, -4, 3, 5]

try:

nll1 = calculate_NLL(X2, y2, betas1)

nll2 = calculate_NLL(X2, y2, betas2)

except:

print('Function results in an error.')

return

try:

nll1 = float(nll1)

nll2 = float(nll2)

except:

print('Returned value has non-numerical data type.')

return

check1 = round(nll1, 2) == 450.23

check2 = round(nll2, 2) == 118.16

if not (check1 and check2):

print('NLL score returned is incorrect.')

return

print('All tests passed.')

X1, y1, X2, y2 = generate_values()

-------

def generate_values():

import numpy as np

from sklearn.datasets import make_classification

N = 1000

np.random.seed(1)

x1 = np.random.normal(500, 100, N).astype(int)

np.random.seed(597474)

ep = np.random.normal(0, 0.75, N)

y1 = 16 * (x1/1000) ** 5.8 * np.exp(ep)

y1 = y1.round(4)

X2, y2 = make_classification(n_samples=1000, n_classes=3, n_features=100, n_informative=20,

n_redundant=10, class_sep=1.6, random_state=16)

np.random.seed(1)

X3 = np.random.normal(100, 20, size=(100,5))

betas = np.array([15, 32, 4.5, -27, -17.5])

y3 = X3 @ betas + np.random.normal(0, 400, 100)

X3_ones = np.hstack([np.ones((100,1)), X3])

return x1, y1, X2, y2, X3, y3, X3_ones

x1, y1, X2, y2, X3, y3, X3_ones = generate_values()

------------------python: needing help with code below- shape of array not returned correct *************

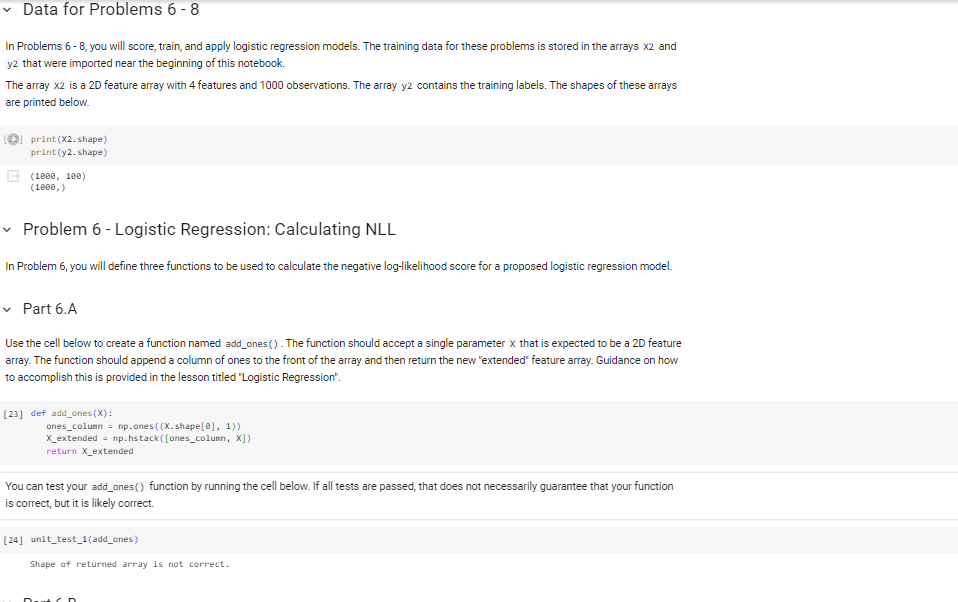
function returns error***********

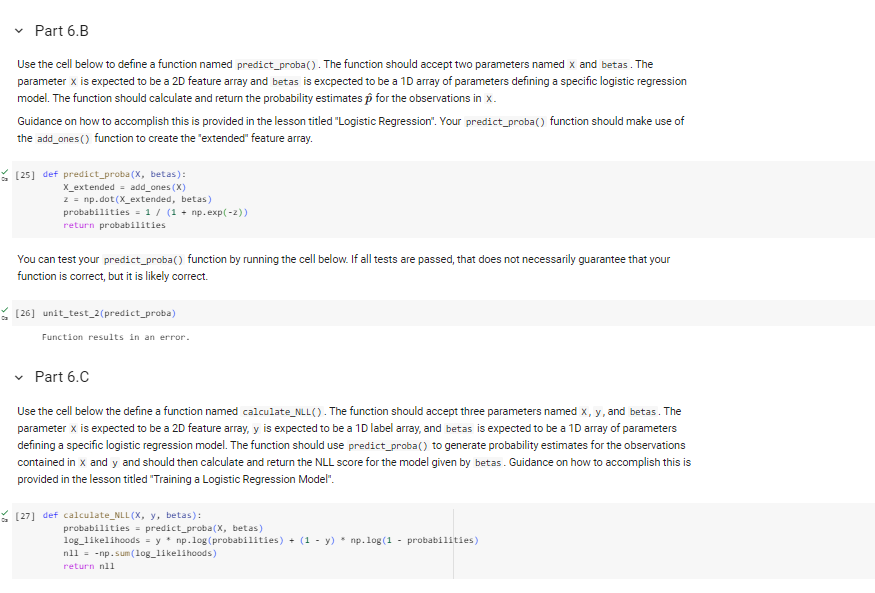
error below

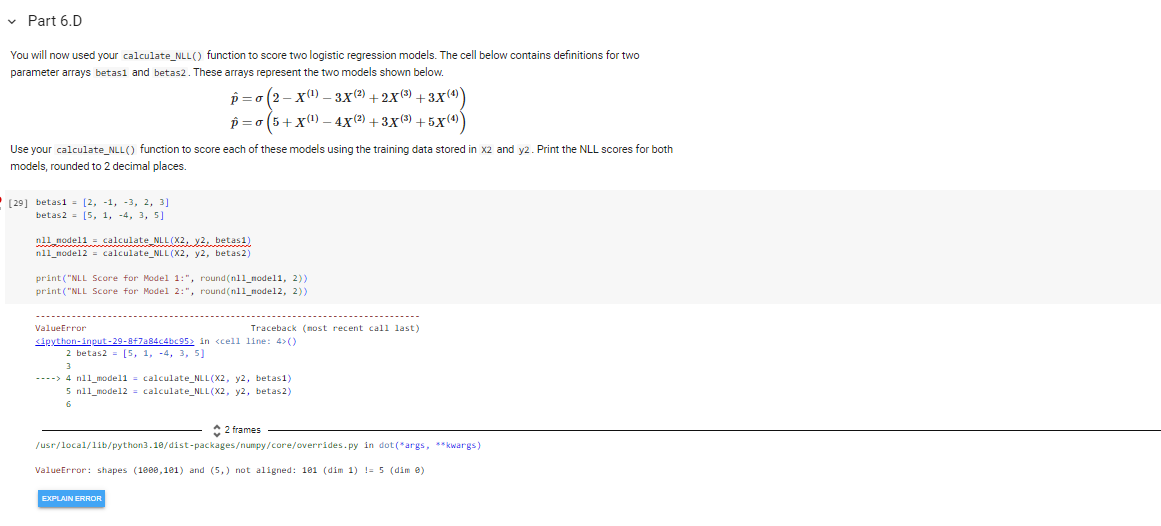In Problems 6-8, you will score, train, and apply logistic regression models. The training data for these problems is stored in the arrays x2 and y2 that were imported near the beginning of this notebook. The array X2 is a 2D feature array with 4 features and 1000 observations. The array y2 contains the training labels. The shapes of these arrays are printed below. print( x2. shape) print(y2. shape) (1000,100) (1000, Problem 6 - Logistic Regression: Calculating NLL In Problem 6, you will define three functions to be used to calculate the negative log-likelihood score for a proposed logistic regression model. Part 6.A Use the cell below to create a function named add_ones (). The function should accept a single parameter x that is expected to be a 2D feature array. The function should append a column of ones to the front of the array and then return the new "extended" feature array. Guidance on how to accomplish this is provided in the lesson titled 'Logistic Regression". [23] def add_ones (X) : ones_colum = np.ones ((X. shape [],1)) X_extended = np.hstack([ones_colum, x]) return X_extended You can test your add_ones() function by running the cell below. If all tests are passed, that does not necessarily guarantee that your function is correct, but it is likely correct. [24] unit_test_1(add_ones) Shape of returned array is not correct. Part 6.B Use the cell below to define a function named predict_proba(). The function should accept two parameters named x and betas . The parameter x is expected to be a 2D feature array and betas is excpected to be a 1D array of parameters defining a specific logistic regression model. The function should calculate and return the probability estimates p^ for the observations in x. Guidance on how to accomplish this is provided in the lesson titled "Logistic Regression". Your predict_proba() function should make use of the add_ones() function to create the "extended" feature array. [25] def predict_proba( X, betas) : X_extended = add_ones (X) z=np.dot(X_extended, betas) probabilities =1/(1+npexp(2)) return probabilities You can test your predict_proba() function by running the cell below. If all tests are passed, that does not necessarily guarantee that your function is correct, but it is likely correct. [26] unit_test_2(predict_proba) Function results in an error. Part 6.C Use the cell below the define a function named calculate_NLL(). The function should accept three parameters named x,y, and betas. The parameter x is expected to be a 2D feature array, y is expected to be a 1D label array, and betas is expected to be a 1D array of parameters defining a specific logistic regression model. The function should use predict_proba() to generate probability estimates for the observations contained in x and y and should then calculate and return the NLL score for the model given by betas. Guidance on how to accomplish this is provided in the lesson titled "Training a Logistic Regression Model". [27] def calculate_NLL(X, y, betas): probabilities = predict_proba( X, betas ) log1 ikelihoods =y np.log(probabilities )+(1y)nplog(1 probabilities ) n11 = -np.sum(1og_1ikelihoods) return n11 You will now used your calculate_NLL() function to score two logistic regression models. The cell below contains definitions for two parameter arrays betas 1 and betas 2 . These arrays represent the two models shown below. p^=(2X(1)3X(2)+2X(3)+3X(4))p^=(5+X(1)4X(2)+3X(3)+5X(4)) Use your calculate_NLL() function to score each of these models using the training data stored in x2 and y2. Print the NLL scores for both models, rounded to 2 decimal places. [29] betas1 =[2,1,3,2,3] betas 2=[5,1,4,3,5] n11 rode11 = calculate NLL (x2,y2, betas1) n11_node12 = calculate_NLL (X2, y2, betas 2) print("NLL Score for Mode1 1:", round(n11_node11, 2)) print("NLL Score for Mode1 2:", round(n11_node12, 2)) ValueError Traceback (nost recent call last) Sipython-input-29-8+7a84c4bc95> in 4>() 2 betas 2=[5,1,4,3,5] 3 ...- 4 n11_mode11 = calculate_NLL (X2, y2, betas1) 5 n11_mode12 = calculate_NLL(X2, y2, betas 2) 6 2 frames /usr/local/11b/python3.10/dist-packagesumpy/core/overrides.py in dot(*args, **kwargs) ValueError: shapes (1000,101) and (5,) not aligned: 101 (dim 1) != 5 (dim e)