Define the degree of a vertex of an undirected graph as the number of edges incident on that vertex. Prove that an undirected graph must have an even number of vertices of odd degree.

1. Here is the complement of the graph above the graph with all its edges reversed. Do DFS on this graph following Kosarajus algorithm as shown in the notes, the text, or geeksforgeeks.org (same result). Show the start and finish times in the table below.

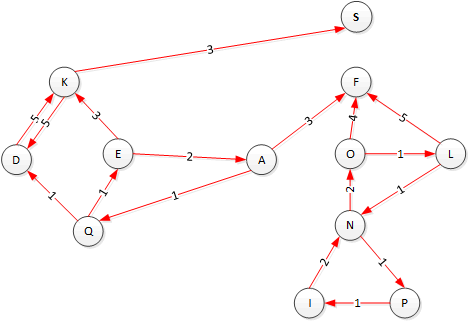
Vertex

A

D

E

F

I

K

L

N

O

P

Q

S

Discovery Time

1

Finishing Time

1. Based on the results of the algorithm, list the SCCs of this graph, one per line below (you may not need all the lines)

_______________________

_______________________

_______________________

_______________________

_______________________

_______________________