Deliverable

For each of the problems shown below, clearly define what the output, input and processing tasks should be to meet the requirements you have been given.

Upload your homework file as a .pdf file to Canvas before the due date specified on Canvas. Late homework will not be accepted.

PROBLEMS

(10 pts) A program determines the position n of a particular number in the Fibonacci sequence. Fibonacci numbers F_n are defined by the recursive relation[1] below. It is assumed that the F_n provided is a valid Fibonacci number.

where the initial seeds are F₀ = 0 and F₁ = 1. The following table shows the position n of the first six numbers F_n in the Fibonacci sequence (including the seeds 0 and 1);

Position (n)	0	1	2	3	4	5
Fibonacci number (Fn)	0	1	1	2	3	5

The formula to calculate the position n of a Fibonacci number F_n in the Fibonacci sequence is:

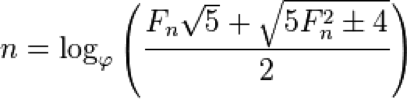
is the golden ratio.

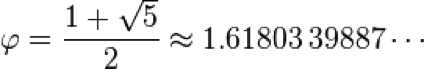
Equation (1) will be evaluated twice (i.e., once with +4, and once with -4) and only integer solutions can be used to represent the position n of a Fibonacci number F_n. (Hint: The logarithm change-of-base formula can help simplify complicated logarithm functions.)

[1] https://en.wikipedia.org/wiki/Fibonacci_number

A program determines the position n of a particular number in the Fibonacci sequence. Fibonacci numbers Fn are defined by the recursive relation[1] below. It is assumed that the Fn provided is a valid Fibonacci number. where the initial seeds are F_0 = 0 and F_1 = 1. The following table shows the position n of the first six numbers F_n in the Fibonacci sequence (including the seeds 0 and 1): The formula to calculate the position n of a Fibonacci number F_n in the Fibonacci sequence is: n = log_phi (F_n Squareroot 5 + Squareroot 5 F_n ^2 plusminus 4/2) is the golden ratio. phi = 1 + Squareroot 5/2 almostequalto 1.6180339887 .. Equation (1) will be evaluated twice (i.e., once with +4, and once with -4) and only integer solutions can be used to represent the position n of a Fibonacci number F_n