Determine the minimum number of moves required for moving N disks from source to destination using a closed form formula. not recursion

above is the recurrence formula. I NEED TO Determine the minimum number of moves required for moving N disks from source to destination using a closed form formula.

if you know how to code then it would be great if you can implement the closed for formula into a C program but not necessary.

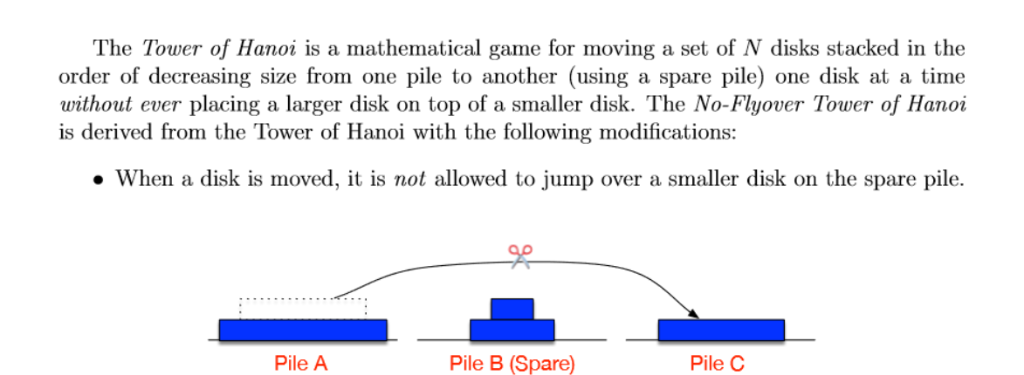
The Tower of Hanoi is a mathematical game for moving a set of N disks stacked in the order of decreasing size from one pile to another (using a spare pile) one disk at a time without ever placing a larger disk on top of a smaller disk. The No-Flyover Tower of Hanoi is derived from the Tower of Hanoi with the following modifications: When a disk is moved, it is not allowed to jump over a smaller disk on the spare pile. Pile A Pile B (Spare Pile C Problem is quite interesting since no flyover restriction is imposed and hence to keep n disks pile A to pile B, we will use following strategy now 1. Move n-1 disk from pile A to pile C 2. Move the single disk from pile A to pile B. 3. Move n-1 disk from ple C to pile A since this is allowed 4. Move the single disk on pile B to pile C 5. Move all n-1 disks from pile A to C Thus in the above 5 step, we will be able to move all n disks from pile A to C while maintaining all the constraints. Now this n disk movement is happened by moving n-1 disks 3 times, one time from A to C, one time from C to A and last time from A to C. And single disk movement happened 2 times, one time from A to B and one time from B to C Hence if Hanoi(n) is the number of disk movement needed for the this problem of size n then the recurrence relation will be Hanoi(n) 3*Hanoi(n-1)+2 Hence the recursive algorithm will be int Hanoi(int n) if (n--1) return 1;/base case else return (3*Hanoi(n-1)+2); //This will solve the recurrence Hence the above program in O(n) will compute the value of Hanoi(n) The Tower of Hanoi is a mathematical game for moving a set of N disks stacked in the order of decreasing size from one pile to another (using a spare pile) one disk at a time without ever placing a larger disk on top of a smaller disk. The No-Flyover Tower of Hanoi is derived from the Tower of Hanoi with the following modifications: When a disk is moved, it is not allowed to jump over a smaller disk on the spare pile. Pile A Pile B (Spare Pile C Problem is quite interesting since no flyover restriction is imposed and hence to keep n disks pile A to pile B, we will use following strategy now 1. Move n-1 disk from pile A to pile C 2. Move the single disk from pile A to pile B. 3. Move n-1 disk from ple C to pile A since this is allowed 4. Move the single disk on pile B to pile C 5. Move all n-1 disks from pile A to C Thus in the above 5 step, we will be able to move all n disks from pile A to C while maintaining all the constraints. Now this n disk movement is happened by moving n-1 disks 3 times, one time from A to C, one time from C to A and last time from A to C. And single disk movement happened 2 times, one time from A to B and one time from B to C Hence if Hanoi(n) is the number of disk movement needed for the this problem of size n then the recurrence relation will be Hanoi(n) 3*Hanoi(n-1)+2 Hence the recursive algorithm will be int Hanoi(int n) if (n--1) return 1;/base case else return (3*Hanoi(n-1)+2); //This will solve the recurrence Hence the above program in O(n) will compute the value of Hanoi(n)