Discuss the Beta results of the calculation. What does it mean? Does it make sense to you with what you know about Coca Cola?

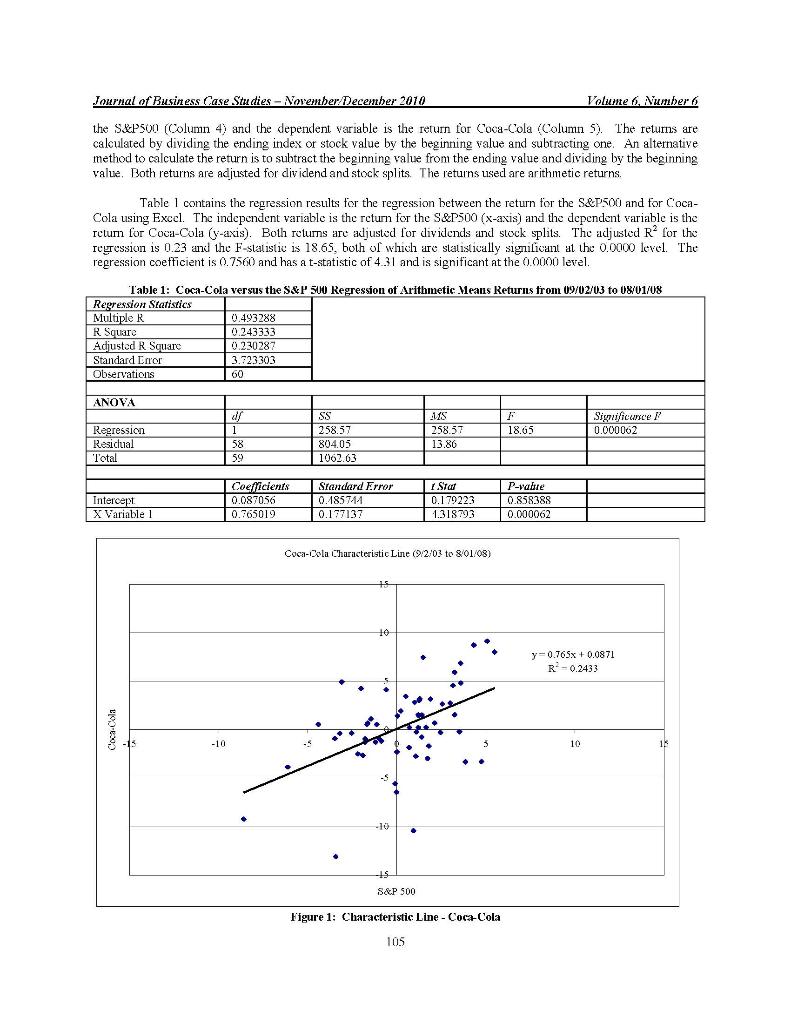


Journal of Business Case Studies - November December 2010 Volume 6Number 6 Calculating The Beta Coefficient And Required Rate Of Return For Coca-Cola Jolu C. Gardner, University of New Orleans, USA Carl B. McGowan, Jr., Norfolk State University, USA Susan E. Moller, Eastcin Michigari University, USA ABSTRACT In this paper, we demonstrate how to compute the required rate of return for Coca-Cola using modern portfolio theory with data downloaded from the intemet. We denonstrate how to calculate monthly returns for the index and Coca-Cola and how to use the returns to compute the hetu coefficient and the required rate of retum using the downloaded data. Fe show how to validate the data for the market index and the company and how to compute the retums using the dividend and stock split adjusted prices. Ite demonstrate how to graph the characteristic line for Coca-Cola and use the graph to check that the regression was pun correctly. We use Coca-Cola and the S&P 500 Index in this paper, but my company listed on Yahoo! Finance can be used as the example. This paper can be used as the basis of a lecture on intermediate corporale finance or investments to demonstrate the process using a real company. Keywords: beta: characteristic line; required rate of return; Coca-Cola: lcaching noto INTRODUCTION M arkowitz' (1952) began modern portfolio theory (MPT) which can be used to explain the relationship between risk and return for assets, particularly stocks. Stock of companies that have higher rates of return have higher levels of risk. order to achieve a lower level of risk, an investor must accept a lower expected rate of return. This concept is called dominance principle and allows for the creation of the cfficicnt frontier. MIT partitions risk into non-systematic risk, which can be climinated from a portfolio through diversification, and systematic risk that is market wide and cannot be diversificu. Non-systematic risk is company specific and is reduced w zero in a large, well diversified portfolio. In order to determine systematic risk for a stock, we use the market model developed by Sharpe (1964). The returns for a stock are regressed as the dependent variable against a market index used as the independent variable. The slope coefficient of the regression is the measure of systematic risk for the stock Systematic risk measures the degree to which a stock moves with the market A higher beta coefficient implies that returns for the stock move more than the market and a lower beta coefficient implies that returns for the stock move less that the market. The former are aggressive stocks and the latter are defensive stocks. In this paper, we show how to retrieve data from the internet, how to compute retums for both the market index and the stock, and how to run a regression to determine the bela coefficient to measure the systematic risk for the stock. In addition we show how to graph the data with a trend line and statistics to verify that the first regression is run correctly; that is, with the correct variable as the independent variable. We show how to do all of this analysis using Excel Markowitz, received The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990 Sharpe received The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990. 103 Journal of Business Case Studies - November December 2010 Volume 6Number 6 DOWNLOADING DATA FROM THE INTERNET The data used for the analysis discussed in this paper are downloaded from the internet using the Yahoo! Finance website. The URL for Yahoo! Finance is http://finance.yahoo.com Once one arrives at the Yahoo! Finance website, the S&P 500 data can be found by clicking on the S&P507" icon and then clicking on the Historical Prices" icon. Click on the "Monthly" indicator to download monthly data and enter the dates. For this paper we download sixty-one monthly, observations in order to calculate sixty monthly returns. The data columns are: Dato, Open, High, Low, Close, Average Volunc, and Adjusted Close. The index and the Coca-Cola price arc adjusted for splits and dividends. Move the cursor to the bottom of the data and click on "Download to Spreadsheet". Save the data to a spreadsheet and repeat the process for the Coca-Cola data. Begin by entering the Coca-Cola ticker symbol. KO and download and save the data for the save time period. CALCULATING RETURNS FOR TITE S&P 500 INDEX AND FOR COCA-COLA3 In this paper, we use arithmetic returns to compute the bela coefficient for Coca-Cola. Arithmetic retums are calculated by dividing the ending index or stock value, (Value.), by the beginning value, (Valueo), and subtracting one as in Equation [1]. An alternative method to calculate the return is to subtract the beginning value. (Values), from the ending value. (Value,) and dividing by the beginning value (Values), as in Equation [21. Both returns are adjusted for dividends and stock splits. The returns used in the regression analysis are arithmetic returns. Return = [(Value - Value) 1] Return - [(Value - Valuce)/Values)] Five years or Monthly data are used to generale sixiy dala points! CALCULATING BETA POR COCA-COLAS Modem Portfolio Theory shows that investors are rewarded for the systenatic risk of an investment and not for the total risk of an investment because total risk mcludes firm specific risk that can be eliminated in a well diversified portfolio. The specific risk of an individual stock is the slope coefficient of the characteristic line which is the regression line between the monthly returns for the individual security and the monthly returns for the market index Beta coefficient lines are calculated using a sixty month regression. In this example, the beta coefficient for Coca-Cola is calculated using sixty monthly observations of returns for Coca-Cola from 09/02:2003 to 08:01/2008 and returns for the S&P 500) Index for the same time period Beta is the covariance between retums for Coca-Cola and returns for the S&P 500 divided by the variance for the S&P 500. Betako Rko Alphako - Betako (R.) [3] RO the return for Coca-Cola stock the slope of the regression line between returns for the market and returns for Coca-Cola Alpha ko the intercept coefficient for the regression line between returns for the market and returns for Coca- Cola (Rm) the return on the S&P 500 Stock market Index (Rm-R) the market risk premium is the additional return that stock holders receive for the additional risk of holding stocks rather than the risk free asset. long-term government bonds. Appendix A contains the data used to compute the Coca-Cola bela and are downloaded from Yahoo! Finance. Colunn 1 shows the date and Columns 2 and 3 contain the stock split and dividend adjusted index and price values for the S&P 500 Index and for Coca-cola stock, respectively. The independent variable is the return for Sce Brigham and Ehrhardt (2008, pages 223-225) for a discussion of how to compute a beta coefficient 4 See Brigham and Ehrhardt (2008, page 223). See Brigham and Ehrhardt (2008, pages 223-225) for a discussion of how to compute a beta coefficient. 104 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 the S&P500 (Column 4) and the dependent variable is the return for Coca-Cola (Column 5). The returns are calculated by dividing the ending index or stock value by the beginning value and subtracting one. An alternative method to calculate the return is to subtract the beginning value from the ending value and dividing by the beginning value. Both returns are adjusted for dividend and stock splits. The returns used are arithmetic returns. Table 1 contains the regression results for the regression between the return for the S&P500 and for Coca- Cola using Excel. The independent variable is the return for the S&P500 (x-axis) and the dependent variable is the Telum for Coca-Cola (y-axis). Both returns are adjusted for dividends and stock splits. The adjusted R for the regression is 0.23 and the F-statistic is 18.65, both of which are statistically significant at the 0.0000 level. The regression coefficient is 0.7500 and has a t-statistic of 431 and is significant at the 0.0000 level. Table 1: Coca-Cola versus the S&P 500 Regression of Arithmetic Means Returns from 09/02/03 08/01/08 Regression Statistics Multiple R 0.493288 R Square 0.243333 Adjusted R Square 0.230287 Standard Error 3.723303 Observations 60 ANOVA F 18.65 Significurce ? 0.000062 Regression Resichual Total df 1 58 59 11S 258.57 13.86 SS 258.57 80403 1062.63 1 Star Intercept X Variable 1 Coeficients 0.087056 0.765019 Standard Error 0.185744 0.137137 0.179223 1.318793 P-vakre 0.858388 0.000062 Coca-Cola Characteristic Line 2:03 to 8/01/08) 15 10 y=0.765x + 0.0871 R? -0.2433 Coca-Cola -10 10 15 -10) -15 S&P 500 Figure 1: Characteristic Line - Coca-Cola 105 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 Figure 1 is a graph of the data used to compute the Coca-Cola beta, which is the characteristic line for Coca-Cola, l'igure I was created in Excel using the Chart function The independent variable is the return for the S&P500 (x-axis) and the dependent variable is the return for Coca-Cola (y-axis). Both returns are adjusted for dividends and for stock splits. The chart contains the trend line and R. The statistics in the graph are the same as the regression statistics in Table 1. The pedagogical purpose of the graph is to chart the characteristic line for Coca- Cola and to confirm that the regression was run with the correct independent and dependent variable. If the trend line and statistics in the graph are not identical to the numbers in the regression, the student has reversed the Variables CALCULATING THE REQUIRED RATE OF RETURN FOR STOCKS Graham and Harvey (2002) find that 73.5 percent of respondents to their survey indicate that the company of the survey respondent uses the capital asset pricing model (CAPMI) to detenuine the component cost of common stock equily capital . In this paper, we use the CAPM 10 compute the required rate of relum for Coca-Cola. The required rate of return for Coca-Cola is the minimum rate of relum demanded by stockholders of Coca-Cola stock. The model used in this paper is based on the CAPM derived from the work of Sharpe (1964). Rko = Rr1 Betaco (R-R) 541 RKO RE Batago Ra (Ron-R) = the required rate of return for Coca-Cola Stock - the risk free rate of return the beta coefficient for Coca-Cola the rate of retum on the stock market the market risk premium The required rate of return for Coca-Cola is the risk-free rate of return plus the risk premium for Coca- Cola. The risk premium is the beta for Coca-Cola time the market price of risk. COMPUTING THE REQUTRED RATE OF RETURN FOR COCA-COLA (KO) USING THE CAPV The risk free rate is the total return (income plus capital appreciation) on Long-term Government Bonds taken from SBBI 2007 For the years from 1926 to 1976, SBBI uses the Government Bond Filc from the Center for Research in Security Prices. For the period from 1976 to 2006, the returns in SBBI 2007 are computed from data taken from the Wall Street Journal. The yield for the hond is the discount rate that equates the expected future cash flows, coupon payments and maturity value, to the current price. Table 2 contains a summary of the input data and sources of that data. Table 2: Input Data and Sources Value Variable Betake R Ra 0.7650 0.0580 0.1230 0.1077 Source Coniputed SBBI, 2007, page 31 SBBI, 2007, page 31 Computer We use the security market line to compute the required rate of return for Coca-Cola. We use the long- krni bond rate taken from SBBI (2007) which cquals 5.8% and the long-term market return of 12.3%. The market Tisk prensiuni is 6.5%. This yields a cost of equity for Coca-Cola of 10.77% * See Ross, Westerfield, and Jordan (2008, page 483) See Brigham and Ehrhardt (2008, pages, 226-228) and Ross, Westerfield, and Jordan (2008, pages 126-127). *Stocks, Bonds, Bills, and Inflation Market Results for 1936-2006, 2007 Yearbook, Classic Friition. Momingstar, 2007. 106 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 Rxo - Ri+ Betako (R-R:) [5] 10.771% = 5.8% 07650 (12.3%-5.8%) 10.77% = 5,8% 10.7650 (6.5") 10.77% = 5.8%+4.97% The required rate of return for Coca-Cola stock is 10.77%. SUMMARY AND CONCLUSIONS In this paper, we demonstrate how to compute the required rate of return for Coca-Cola using modem portfolio theory. Data is downloaded from Yahoo! Finance for both Coca-Cola and for the S&P 500 Index. The adjusted stock price for Coca-Cola and the S&P 500 Index are used to compute a five-year, monthly series of Telums. The characteristic line is the regression line from the regression in which the nonthly retunis for the S&P 500 Index are the independent variables and the monthly returns for Coca-Cola are the dependent variables. The regression is run using the Data Analysis Tool Pak in Excel and the Chart function We use SBRI 2007 data to compute the required rate of return using the market model We compute a required rate of return for Coca-Cola equal to 10.77% The objective of this paper is to demonstrate how to download the data needed to compute the required rate of return for Coca-Cola using Modern Portfolio Theory: We demonstrate how to calculate monthly returns for the index and Coca-Cola and how to use the returns to compute the beta coefficient and the required rate of retum using the downloaded data. We show how to validate the data for the market index and the company and how to compute the returns using the dividend and stock split adjusted prices. We demonstrate how to graph the characteristic line for Coca-Cola and use the graph to check that the regression was run correctly. We use Coca-Cola and the S&P 500 Index in this paper, but any company listed on Yahoo! l'inance can be used as the example. This paper can be used as the basis of a lecture on intermediate corporate finance or investments to demonstrate the process using a real company. ALTTIOR INFORMATION John C. Gardner is the KPMG Professor of Accounting and Director of the Global Entrepreneurship Initiative in the Department of Accounling at the University of New Orleans. He canned his undergraduate degree in accounting from SUNY at Albany, and MBA and PhD degrees in finance from Michigan State University. Dr. Gardner has published in leading accounting, finance and management science journals including Accounting Review Journal of Accouming Research Contemporary Accounting Research Accounting, Orgamzations and Society, Joumal of Financial and Quanhlalive Analysis and Decision Sciences. His rescarch interests include multi-national Corporation linancial management, capital structure, and financial and forensic accounting. Carl B. McGowan, Jr., PhD, CFA is a Professor of Finance at Norfolk State University, has a BA in International Relations (Syracuse), an MBA in Finance (Eastern Michigan), and a PhD) in Business Administration (Finance) from Michigan State. From 2003 to 2004, he held the RHB Bank Distinguished Chair in Finance at the Lniversiti Kebangsaan Malaysia and has taught in Cost Rica, Malaysia, Moscow, Saudi Arabia, and The UAE. Professor McGowan has published in numerous journals including Applied Financial Ticonomics. Decision Science. Financial Practice and Education, The Financial Review. Inte mational Business and Econonjes Research Joumal, The Intemotional Review of Financial Analysis, Journal of Applied Business Research. The Journal of Business Case Studies, The Joumal of Diversity Management, The Journal of Real Estate Research, Managerial l'inance, Managing Global Transitions The Southwestern Economic Review, and Urban Studies. Susan E. Moeller is a Professor of Finance at Eastern Michigan University since 1990. Prior to joining EMU, Dr. Moeller taught at Northeastern University in Boston and at the University of Michigan - Flint. Ter corporate experience was Ford Motor Company. She has published in a number of journals including of Fconomic and Financial F.discation, Journal of Business Cose Studies, Journal of Global Business , Journal of International Finance, Journal of Financial and Strategic Decisions Management International Review: Joumai of ipplied Business Research and XII Joumal. 107 Journal of Business Case Studies - November December 2010 Volume 6, Number 6 APPENDIX A Date 8:1.2008 7:1/2008 62/2008 5:1/2008 4.41/2008 3:3/2008 2:1/2008 1.2.2008 12/3/2007 11/1/2007 10/1/2007 9:1.2007 8.1/2007 7.2.2007 6:1/2002 S11.2007 4:2:2007 3/1/2002 2:1:2007 1:3/2002 12/1/2004 11/1/2006 10/2/2006 9:1/2006 8.1.2006 7/3/2006 6:1/2006 5:1/2006 4:3/2006 3/1/2006 2:1:2006 1.3.2006 12/1/2005 11/1/2005 10/3/2005 9:1.2005 8.1.2005 7:1:2005 6:1/2005 5/2/2005 1.1.2005 3:1/2005 2:1:2005 1:3/2005 12/1/2004 11/1/2004 101/2001 9:1:2004 8.2.2001 7.1.2004 6.1.2004 5:3 2004 4/1/2004 3.1/2001 2:2/2004 1.2.2001 12/1/2003 11/3/2003 10/1/2003 9:2/2003 8.1.2003 120.20 Rates of Return S&P500 ani COCA-COLA S&P500 KO RSAMA 1249.01 S2.07 -1.45 1267.38 51 50 -0.99 1280.00 51 98 -8,60 1 100.38 57.26 1.07 1389.59 58.87 4.75 1322.70 60.87 -0.60 1330.63 58/16 -3.48 1378.99 59.00 -6.12 1468.36 61 37 -0.86 1181.14 62.10 - 1.10 1549.38 61.76 1.48 1926.75 $7.17 3.58 1473.99 53.78 1.29 1459.27 $2.11 -3.20 1503.39 5231 -1.78 1930.62 $299 3.27 1482.37 52.19 -1.33 1420.86 48.00 1.00 1106.82 16.68 -2.18 1438.24 4. 88 1.41 1118.30 18.25 1.26 1400.63 46.83 1.65 1377.94 16.72 3.15 1335.85 44.68 2.46 1303.82 11.81 2.13 1276.66 44 50 0.51 13.02 0.01 1270.09 44.03 -3.09 1310.61 11.96 1.22 1294.87 41 87 1.11 1280.66 4197 0.05 1280.08 11 38 2.55 1248.29 4031 -0.10 12.19.18 12.69 3.52 1207.01 42.78 -1.77 1228.81 13.19 1.69 1220.33 14.00 -1.12 1234.18 13.76 3.60 1191.33 41.75 -0.01 1191.90 44.63 3.00 1196.85 13.11 -2.01 1180.59 41.67 -1.91 1203.60 12.80 1.89 1181.27 41.49 -2.53 1211.92 41.64 1173.82 3931 3.86 1130.20 10.66 1.10 1114.58 400S 0.94 1101.24 14.71 0.23 1101.72 43.86 -3.43 1140,84 S0.48 1.80 1120.6% 5135 1.21 1107.30 SOST -1.68 1126.21 5030 -1.61 1144.94 4996 1.22 1131.13 19.21 1.73 1111.92 50.75 5.08 10S8.20 160 0.71 1050.71 46.40 5.50 999.97 4296 -1.19 1008.01 4352 Rko 1.11 -0.92 -9.22 -2.73 -3.29 4.12 -0.92 -3.86 -1.18 0.55 1.46 6.86 3.30 -0.38 -1.28 1.53 8.73 2.83 - 2.51 -0.77 3.03 0.24 4.57 -0.29 0.70 3.44 -2.29 4.93 0.21 -0.24 1.43 2.65 -5.58 -0.21 -0.95 -1.84 0.55 481 -6.45 2.74 1.25 -2.64 3.16 -0.36 3.29 5.93 -3.32 1.52 -10.42 1.91 -13.11 -1.69 1.31 0.34 0.68 1.46 -2.98 9.14 8.01 -1.29 109 Journal of Business Case Studies - November December 2010 Volume 6Number 6 Calculating The Beta Coefficient And Required Rate Of Return For Coca-Cola Jolu C. Gardner, University of New Orleans, USA Carl B. McGowan, Jr., Norfolk State University, USA Susan E. Moller, Eastcin Michigari University, USA ABSTRACT In this paper, we demonstrate how to compute the required rate of return for Coca-Cola using modern portfolio theory with data downloaded from the intemet. We denonstrate how to calculate monthly returns for the index and Coca-Cola and how to use the returns to compute the hetu coefficient and the required rate of retum using the downloaded data. Fe show how to validate the data for the market index and the company and how to compute the retums using the dividend and stock split adjusted prices. Ite demonstrate how to graph the characteristic line for Coca-Cola and use the graph to check that the regression was pun correctly. We use Coca-Cola and the S&P 500 Index in this paper, but my company listed on Yahoo! Finance can be used as the example. This paper can be used as the basis of a lecture on intermediate corporale finance or investments to demonstrate the process using a real company. Keywords: beta: characteristic line; required rate of return; Coca-Cola: lcaching noto INTRODUCTION M arkowitz' (1952) began modern portfolio theory (MPT) which can be used to explain the relationship between risk and return for assets, particularly stocks. Stock of companies that have higher rates of return have higher levels of risk. order to achieve a lower level of risk, an investor must accept a lower expected rate of return. This concept is called dominance principle and allows for the creation of the cfficicnt frontier. MIT partitions risk into non-systematic risk, which can be climinated from a portfolio through diversification, and systematic risk that is market wide and cannot be diversificu. Non-systematic risk is company specific and is reduced w zero in a large, well diversified portfolio. In order to determine systematic risk for a stock, we use the market model developed by Sharpe (1964). The returns for a stock are regressed as the dependent variable against a market index used as the independent variable. The slope coefficient of the regression is the measure of systematic risk for the stock Systematic risk measures the degree to which a stock moves with the market A higher beta coefficient implies that returns for the stock move more than the market and a lower beta coefficient implies that returns for the stock move less that the market. The former are aggressive stocks and the latter are defensive stocks. In this paper, we show how to retrieve data from the internet, how to compute retums for both the market index and the stock, and how to run a regression to determine the bela coefficient to measure the systematic risk for the stock. In addition we show how to graph the data with a trend line and statistics to verify that the first regression is run correctly; that is, with the correct variable as the independent variable. We show how to do all of this analysis using Excel Markowitz, received The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990 Sharpe received The Sveriges Riksbank Prize in Economic Sciences in Memory of Alfred Nobel 1990. 103 Journal of Business Case Studies - November December 2010 Volume 6Number 6 DOWNLOADING DATA FROM THE INTERNET The data used for the analysis discussed in this paper are downloaded from the internet using the Yahoo! Finance website. The URL for Yahoo! Finance is http://finance.yahoo.com Once one arrives at the Yahoo! Finance website, the S&P 500 data can be found by clicking on the S&P507" icon and then clicking on the Historical Prices" icon. Click on the "Monthly" indicator to download monthly data and enter the dates. For this paper we download sixty-one monthly, observations in order to calculate sixty monthly returns. The data columns are: Dato, Open, High, Low, Close, Average Volunc, and Adjusted Close. The index and the Coca-Cola price arc adjusted for splits and dividends. Move the cursor to the bottom of the data and click on "Download to Spreadsheet". Save the data to a spreadsheet and repeat the process for the Coca-Cola data. Begin by entering the Coca-Cola ticker symbol. KO and download and save the data for the save time period. CALCULATING RETURNS FOR TITE S&P 500 INDEX AND FOR COCA-COLA3 In this paper, we use arithmetic returns to compute the bela coefficient for Coca-Cola. Arithmetic retums are calculated by dividing the ending index or stock value, (Value.), by the beginning value, (Valueo), and subtracting one as in Equation [1]. An alternative method to calculate the return is to subtract the beginning value. (Values), from the ending value. (Value,) and dividing by the beginning value (Values), as in Equation [21. Both returns are adjusted for dividends and stock splits. The returns used in the regression analysis are arithmetic returns. Return = [(Value - Value) 1] Return - [(Value - Valuce)/Values)] Five years or Monthly data are used to generale sixiy dala points! CALCULATING BETA POR COCA-COLAS Modem Portfolio Theory shows that investors are rewarded for the systenatic risk of an investment and not for the total risk of an investment because total risk mcludes firm specific risk that can be eliminated in a well diversified portfolio. The specific risk of an individual stock is the slope coefficient of the characteristic line which is the regression line between the monthly returns for the individual security and the monthly returns for the market index Beta coefficient lines are calculated using a sixty month regression. In this example, the beta coefficient for Coca-Cola is calculated using sixty monthly observations of returns for Coca-Cola from 09/02:2003 to 08:01/2008 and returns for the S&P 500) Index for the same time period Beta is the covariance between retums for Coca-Cola and returns for the S&P 500 divided by the variance for the S&P 500. Betako Rko Alphako - Betako (R.) [3] RO the return for Coca-Cola stock the slope of the regression line between returns for the market and returns for Coca-Cola Alpha ko the intercept coefficient for the regression line between returns for the market and returns for Coca- Cola (Rm) the return on the S&P 500 Stock market Index (Rm-R) the market risk premium is the additional return that stock holders receive for the additional risk of holding stocks rather than the risk free asset. long-term government bonds. Appendix A contains the data used to compute the Coca-Cola bela and are downloaded from Yahoo! Finance. Colunn 1 shows the date and Columns 2 and 3 contain the stock split and dividend adjusted index and price values for the S&P 500 Index and for Coca-cola stock, respectively. The independent variable is the return for Sce Brigham and Ehrhardt (2008, pages 223-225) for a discussion of how to compute a beta coefficient 4 See Brigham and Ehrhardt (2008, page 223). See Brigham and Ehrhardt (2008, pages 223-225) for a discussion of how to compute a beta coefficient. 104 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 the S&P500 (Column 4) and the dependent variable is the return for Coca-Cola (Column 5). The returns are calculated by dividing the ending index or stock value by the beginning value and subtracting one. An alternative method to calculate the return is to subtract the beginning value from the ending value and dividing by the beginning value. Both returns are adjusted for dividend and stock splits. The returns used are arithmetic returns. Table 1 contains the regression results for the regression between the return for the S&P500 and for Coca- Cola using Excel. The independent variable is the return for the S&P500 (x-axis) and the dependent variable is the Telum for Coca-Cola (y-axis). Both returns are adjusted for dividends and stock splits. The adjusted R for the regression is 0.23 and the F-statistic is 18.65, both of which are statistically significant at the 0.0000 level. The regression coefficient is 0.7500 and has a t-statistic of 431 and is significant at the 0.0000 level. Table 1: Coca-Cola versus the S&P 500 Regression of Arithmetic Means Returns from 09/02/03 08/01/08 Regression Statistics Multiple R 0.493288 R Square 0.243333 Adjusted R Square 0.230287 Standard Error 3.723303 Observations 60 ANOVA F 18.65 Significurce ? 0.000062 Regression Resichual Total df 1 58 59 11S 258.57 13.86 SS 258.57 80403 1062.63 1 Star Intercept X Variable 1 Coeficients 0.087056 0.765019 Standard Error 0.185744 0.137137 0.179223 1.318793 P-vakre 0.858388 0.000062 Coca-Cola Characteristic Line 2:03 to 8/01/08) 15 10 y=0.765x + 0.0871 R? -0.2433 Coca-Cola -10 10 15 -10) -15 S&P 500 Figure 1: Characteristic Line - Coca-Cola 105 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 Figure 1 is a graph of the data used to compute the Coca-Cola beta, which is the characteristic line for Coca-Cola, l'igure I was created in Excel using the Chart function The independent variable is the return for the S&P500 (x-axis) and the dependent variable is the return for Coca-Cola (y-axis). Both returns are adjusted for dividends and for stock splits. The chart contains the trend line and R. The statistics in the graph are the same as the regression statistics in Table 1. The pedagogical purpose of the graph is to chart the characteristic line for Coca- Cola and to confirm that the regression was run with the correct independent and dependent variable. If the trend line and statistics in the graph are not identical to the numbers in the regression, the student has reversed the Variables CALCULATING THE REQUIRED RATE OF RETURN FOR STOCKS Graham and Harvey (2002) find that 73.5 percent of respondents to their survey indicate that the company of the survey respondent uses the capital asset pricing model (CAPMI) to detenuine the component cost of common stock equily capital . In this paper, we use the CAPM 10 compute the required rate of relum for Coca-Cola. The required rate of return for Coca-Cola is the minimum rate of relum demanded by stockholders of Coca-Cola stock. The model used in this paper is based on the CAPM derived from the work of Sharpe (1964). Rko = Rr1 Betaco (R-R) 541 RKO RE Batago Ra (Ron-R) = the required rate of return for Coca-Cola Stock - the risk free rate of return the beta coefficient for Coca-Cola the rate of retum on the stock market the market risk premium The required rate of return for Coca-Cola is the risk-free rate of return plus the risk premium for Coca- Cola. The risk premium is the beta for Coca-Cola time the market price of risk. COMPUTING THE REQUTRED RATE OF RETURN FOR COCA-COLA (KO) USING THE CAPV The risk free rate is the total return (income plus capital appreciation) on Long-term Government Bonds taken from SBBI 2007 For the years from 1926 to 1976, SBBI uses the Government Bond Filc from the Center for Research in Security Prices. For the period from 1976 to 2006, the returns in SBBI 2007 are computed from data taken from the Wall Street Journal. The yield for the hond is the discount rate that equates the expected future cash flows, coupon payments and maturity value, to the current price. Table 2 contains a summary of the input data and sources of that data. Table 2: Input Data and Sources Value Variable Betake R Ra 0.7650 0.0580 0.1230 0.1077 Source Coniputed SBBI, 2007, page 31 SBBI, 2007, page 31 Computer We use the security market line to compute the required rate of return for Coca-Cola. We use the long- krni bond rate taken from SBBI (2007) which cquals 5.8% and the long-term market return of 12.3%. The market Tisk prensiuni is 6.5%. This yields a cost of equity for Coca-Cola of 10.77% * See Ross, Westerfield, and Jordan (2008, page 483) See Brigham and Ehrhardt (2008, pages, 226-228) and Ross, Westerfield, and Jordan (2008, pages 126-127). *Stocks, Bonds, Bills, and Inflation Market Results for 1936-2006, 2007 Yearbook, Classic Friition. Momingstar, 2007. 106 Journal of Business Case Studies - November December 2010 Volume 6 Number 6 Rxo - Ri+ Betako (R-R:) [5] 10.771% = 5.8% 07650 (12.3%-5.8%) 10.77% = 5,8% 10.7650 (6.5") 10.77% = 5.8%+4.97% The required rate of return for Coca-Cola stock is 10.77%. SUMMARY AND CONCLUSIONS In this paper, we demonstrate how to compute the required rate of return for Coca-Cola using modem portfolio theory. Data is downloaded from Yahoo! Finance for both Coca-Cola and for the S&P 500 Index. The adjusted stock price for Coca-Cola and the S&P 500 Index are used to compute a five-year, monthly series of Telums. The characteristic line is the regression line from the regression in which the nonthly retunis for the S&P 500 Index are the independent variables and the monthly returns for Coca-Cola are the dependent variables. The regression is run using the Data Analysis Tool Pak in Excel and the Chart function We use SBRI 2007 data to compute the required rate of return using the market model We compute a required rate of return for Coca-Cola equal to 10.77% The objective of this paper is to demonstrate how to download the data needed to compute the required rate of return for Coca-Cola using Modern Portfolio Theory: We demonstrate how to calculate monthly returns for the index and Coca-Cola and how to use the returns to compute the beta coefficient and the required rate of retum using the downloaded data. We show how to validate the data for the market index and the company and how to compute the returns using the dividend and stock split adjusted prices. We demonstrate how to graph the characteristic line for Coca-Cola and use the graph to check that the regression was run correctly. We use Coca-Cola and the S&P 500 Index in this paper, but any company listed on Yahoo! l'inance can be used as the example. This paper can be used as the basis of a lecture on intermediate corporate finance or investments to demonstrate the process using a real company. ALTTIOR INFORMATION John C. Gardner is the KPMG Professor of Accounting and Director of the Global Entrepreneurship Initiative in the Department of Accounling at the University of New Orleans. He canned his undergraduate degree in accounting from SUNY at Albany, and MBA and PhD degrees in finance from Michigan State University. Dr. Gardner has published in leading accounting, finance and management science journals including Accounting Review Journal of Accouming Research Contemporary Accounting Research Accounting, Orgamzations and Society, Joumal of Financial and Quanhlalive Analysis and Decision Sciences. His rescarch interests include multi-national Corporation linancial management, capital structure, and financial and forensic accounting. Carl B. McGowan, Jr., PhD, CFA is a Professor of Finance at Norfolk State University, has a BA in International Relations (Syracuse), an MBA in Finance (Eastern Michigan), and a PhD) in Business Administration (Finance) from Michigan State. From 2003 to 2004, he held the RHB Bank Distinguished Chair in Finance at the Lniversiti Kebangsaan Malaysia and has taught in Cost Rica, Malaysia, Moscow, Saudi Arabia, and The UAE. Professor McGowan has published in numerous journals including Applied Financial Ticonomics. Decision Science. Financial Practice and Education, The Financial Review. Inte mational Business and Econonjes Research Joumal, The Intemotional Review of Financial Analysis, Journal of Applied Business Research. The Journal of Business Case Studies, The Joumal of Diversity Management, The Journal of Real Estate Research, Managerial l'inance, Managing Global Transitions The Southwestern Economic Review, and Urban Studies. Susan E. Moeller is a Professor of Finance at Eastern Michigan University since 1990. Prior to joining EMU, Dr. Moeller taught at Northeastern University in Boston and at the University of Michigan - Flint. Ter corporate experience was Ford Motor Company. She has published in a number of journals including of Fconomic and Financial F.discation, Journal of Business Cose Studies, Journal of Global Business , Journal of International Finance, Journal of Financial and Strategic Decisions Management International Review: Joumai of ipplied Business Research and XII Joumal. 107 Journal of Business Case Studies - November December 2010 Volume 6, Number 6 APPENDIX A Date 8:1.2008 7:1/2008 62/2008 5:1/2008 4.41/2008 3:3/2008 2:1/2008 1.2.2008 12/3/2007 11/1/2007 10/1/2007 9:1.2007 8.1/2007 7.2.2007 6:1/2002 S11.2007 4:2:2007 3/1/2002 2:1:2007 1:3/2002 12/1/2004 11/1/2006 10/2/2006 9:1/2006 8.1.2006 7/3/2006 6:1/2006 5:1/2006 4:3/2006 3/1/2006 2:1:2006 1.3.2006 12/1/2005 11/1/2005 10/3/2005 9:1.2005 8.1.2005 7:1:2005 6:1/2005 5/2/2005 1.1.2005 3:1/2005 2:1:2005 1:3/2005 12/1/2004 11/1/2004 101/2001 9:1:2004 8.2.2001 7.1.2004 6.1.2004 5:3 2004 4/1/2004 3.1/2001 2:2/2004 1.2.2001 12/1/2003 11/3/2003 10/1/2003 9:2/2003 8.1.2003 120.20 Rates of Return S&P500 ani COCA-COLA S&P500 KO RSAMA 1249.01 S2.07 -1.45 1267.38 51 50 -0.99 1280.00 51 98 -8,60 1 100.38 57.26 1.07 1389.59 58.87 4.75 1322.70 60.87 -0.60 1330.63 58/16 -3.48 1378.99 59.00 -6.12 1468.36 61 37 -0.86 1181.14 62.10 - 1.10 1549.38 61.76 1.48 1926.75 $7.17 3.58 1473.99 53.78 1.29 1459.27 $2.11 -3.20 1503.39 5231 -1.78 1930.62 $299 3.27 1482.37 52.19 -1.33 1420.86 48.00 1.00 1106.82 16.68 -2.18 1438.24 4. 88 1.41 1118.30 18.25 1.26 1400.63 46.83 1.65 1377.94 16.72 3.15 1335.85 44.68 2.46 1303.82 11.81 2.13 1276.66 44 50 0.51 13.02 0.01 1270.09 44.03 -3.09 1310.61 11.96 1.22 1294.87 41 87 1.11 1280.66 4197 0.05 1280.08 11 38 2.55 1248.29 4031 -0.10 12.19.18 12.69 3.52 1207.01 42.78 -1.77 1228.81 13.19 1.69 1220.33 14.00 -1.12 1234.18 13.76 3.60 1191.33 41.75 -0.01 1191.90 44.63 3.00 1196.85 13.11 -2.01 1180.59 41.67 -1.91 1203.60 12.80 1.89 1181.27 41.49 -2.53 1211.92 41.64 1173.82 3931 3.86 1130.20 10.66 1.10 1114.58 400S 0.94 1101.24 14.71 0.23 1101.72 43.86 -3.43 1140,84 S0.48 1.80 1120.6% 5135 1.21 1107.30 SOST -1.68 1126.21 5030 -1.61 1144.94 4996 1.22 1131.13 19.21 1.73 1111.92 50.75 5.08 10S8.20 160 0.71 1050.71 46.40 5.50 999.97 4296 -1.19 1008.01 4352 Rko 1.11 -0.92 -9.22 -2.73 -3.29 4.12 -0.92 -3.86 -1.18 0.55 1.46 6.86 3.30 -0.38 -1.28 1.53 8.73 2.83 - 2.51 -0.77 3.03 0.24 4.57 -0.29 0.70 3.44 -2.29 4.93 0.21 -0.24 1.43 2.65 -5.58 -0.21 -0.95 -1.84 0.55 481 -6.45 2.74 1.25 -2.64 3.16 -0.36 3.29 5.93 -3.32 1.52 -10.42 1.91 -13.11 -1.69 1.31 0.34 0.68 1.46 -2.98 9.14 8.01 -1.29 109












