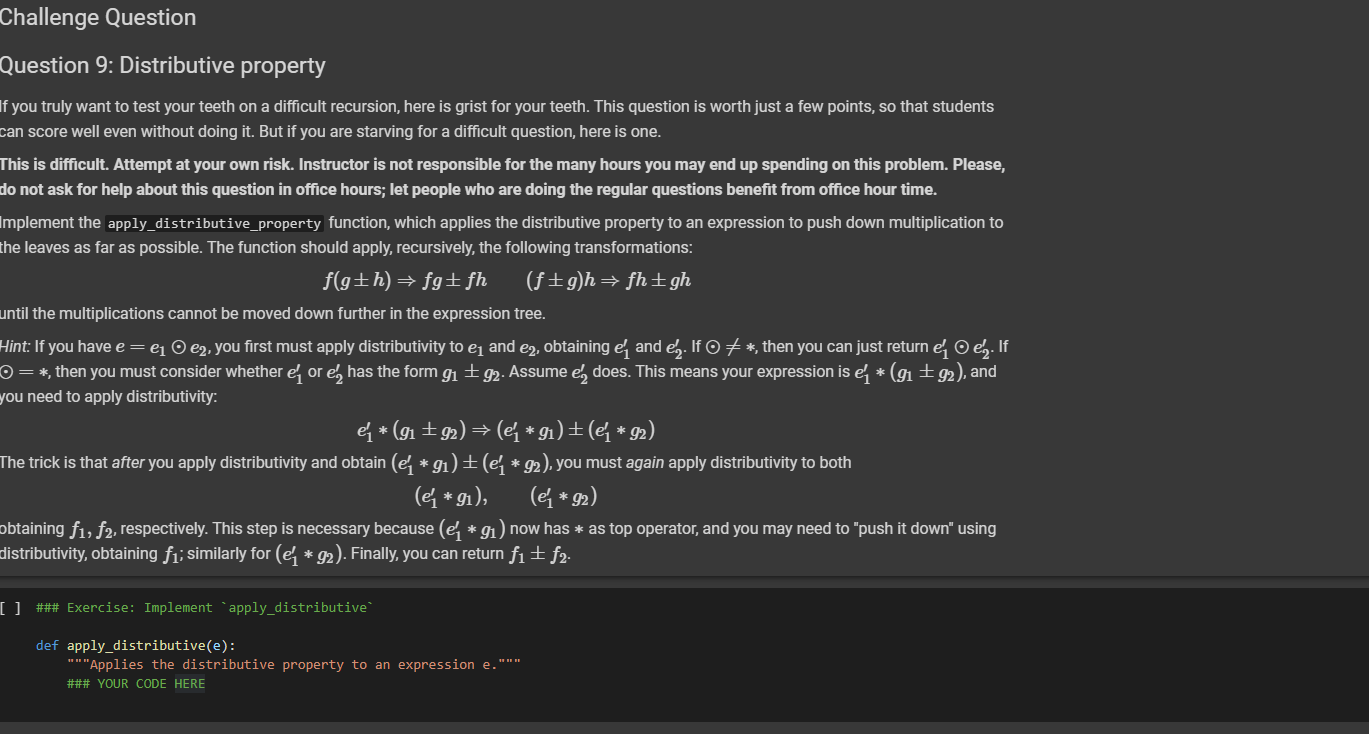
Distributive property in PYTHON
I need help with the code and has to pass the assertion tests
### Exercise: Implement `apply_distributive`
def apply_distributive(e):
"""Applies the distributive property to an expression e."""
### YOUR CODE HERE
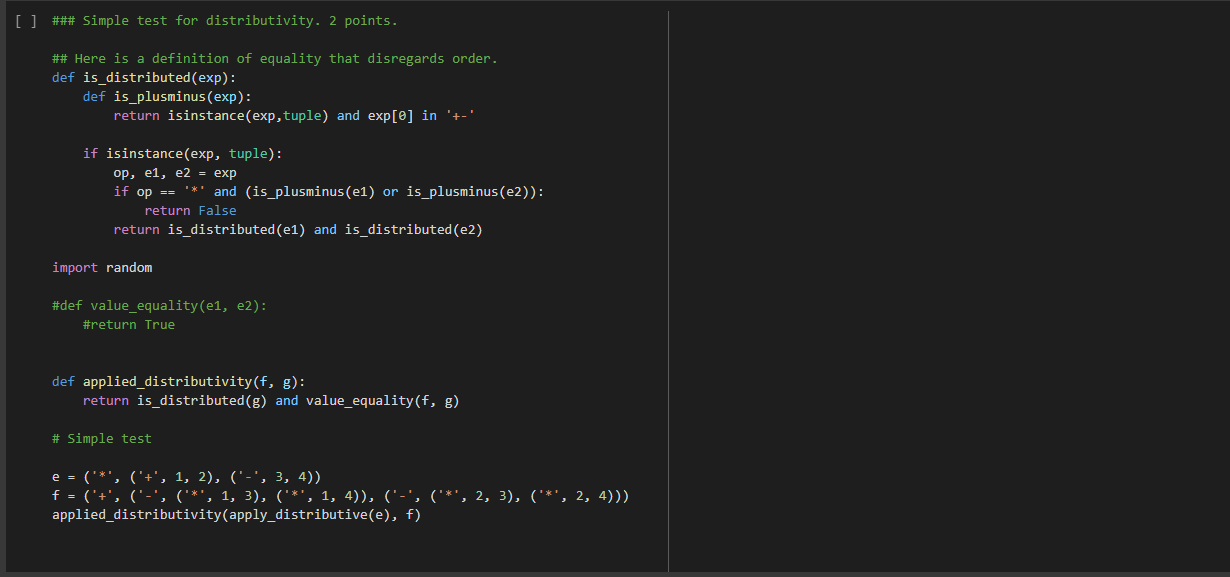
### Simple test for distributivity. 2 points.
## Here is a definition of equality that disregards order.
def is_distributed(exp):
def is_plusminus(exp):
return isinstance(exp,tuple) and exp[0] in '+-'
if isinstance(exp, tuple):
op, e1, e2 = exp
if op == '*' and (is_plusminus(e1) or is_plusminus(e2)):
return False
return is_distributed(e1) and is_distributed(e2)
import random
#def value_equality(e1, e2):
#return True
def applied_distributivity(f, g):
return is_distributed(g) and value_equality(f, g)
# Simple test
e = ('*', ('+', 1, 2), ('-', 3, 4))
f = ('+', ('-', ('*', 1, 3), ('*', 1, 4)), ('-', ('*', 2, 3), ('*', 2, 4)))
applied_distributivity(apply_distributive(e), f)
### More complicated tests for distributivity. 2 points.
# More complex tests
e = ('*', ('+', 1, 2), ('-', 3, 4))
e2 = ('*', e, ('+', 5, 6))
f = ('+',
('-',
('+', ('*', ('*', 1, 3), 5), ('*', ('*', 1, 3), 6)),
('+', ('*', ('*', 1, 4), 5), ('*', ('*', 1, 4), 6))),
('-',
('+', ('*', ('*', 2, 3), 5), ('*', ('*', 2, 3), 6)),
('+', ('*', ('*', 2, 4), 5), ('*', ('*', 2, 4), 6))))
applied_distributivity(apply_distributive(e2), f)
e = ('*', ('*', ('+', 1, 2), ('-', 3, 4)), ('*', ('-', 5, 6), ('+', 7, 8)))
f = ('+',
('-',
('-',
('+', ('*', ('*', 1, 3), ('*', 5, 7)), ('*', ('*', 1, 3), ('*', 5, 8))),
('+', ('*', ('*', 1, 3), ('*', 6, 7)), ('*', ('*', 1, 3), ('*', 6, 8)))),
('-',
('+', ('*', ('*', 1, 4), ('*', 5, 7)), ('*', ('*', 1, 4), ('*', 5, 8))),
('+', ('*', ('*', 1, 4), ('*', 6, 7)), ('*', ('*', 1, 4), ('*', 6, 8))))),
('-',
('-',
('+', ('*', ('*', 2, 3), ('*', 5, 7)), ('*', ('*', 2, 3), ('*', 5, 8))),
('+', ('*', ('*', 2, 3), ('*', 6, 7)), ('*', ('*', 2, 3), ('*', 6, 8)))),
('-',
('+', ('*', ('*', 2, 4), ('*', 5, 7)), ('*', ('*', 2, 4), ('*', 5, 8))),
('+', ('*', ('*', 2, 4), ('*', 6, 7)), ('*', ('*', 2, 4), ('*', 6, 8))))))
applied_distributivity(apply_distributive(e), f)

Challenge Question Question 9: Distributive property If you truly want to test your teeth on a difficult recursion, here is grist for your teeth. This question is worth just a few points, so that students can score well even without doing it. But if you are starving for a difficult question, here is one. This is difficult. Attempt at your own risk. Instructor is not responsible for the many hours you may end up spending on this problem. Please, do not ask for help about this question in office hours; let people who are doing the regular questions benefit from office hour time. Implement the apply_distributive_property function, which applies the distributive property to an expression to push down multiplication to the leaves as far as possible. The function should apply, recursively, the following transformations: f(g+h) = fgfh (f+g)h = fh Egh until the multiplications cannot be moved down further in the expression tree. Hint: If you have e = ej Oe2, you first must apply distributivity to ej and ez, obtaining e' and eq. If 0 + *, then you can just return e Oes. If 0 = *, then you must consider whether e orely has the form 91 +92. Assume el, does. This means your expression is e{ *(91 +92), and you need to apply distributivity: e{*(91 +92) =(e *91)+(@{ *92) The trick is that fter you apply distributivity obtain (@{ *91)+(e* 92), you must again apply distributivity to both (*g), (e *92) obtaining f1, f2, respectively. This step is necessary because (e *91) now has * as top operator, and you may need to "push it down" using distributivity, obtaining fi; similarly for (@{ *92). Finally, you can return f1 + f2. [] ### Exercise: Implement apply_distributive def apply_distributive(e): ""Applies the distributive property to an expression e.""" ### YOUR CODE HERE [] ### Simple test for distributivity. 2 points. ## Here is a definition of equality that disregards order. def is distributed (exp): def is_plusminus(exp): return isinstance(exp, tuple) and exp[@] in '+-' if isinstance(exp, tuple): op, e1, e2 = exp if op == '*' and (is_plusminus(el) or is_plusminus(e2)): return False return is_distributed (01) and is_distributed(e2) import random #def value_equality(ei, e2): #return True def applied_distributivity(f, g): return is_distributed(g) and value_equality(f, g) # Simple test e = ('*', ('+', 1, 2), ('-', 3, 4)) f = ('+', ('-', ("*', 1, 3), ("*', 1, 4)), ('-', ("*', 2, 3), ("*', 2, 4))) applied_distributivity(apply_distributive(e), f) [] ### More complicated tests for distributivity. 2 points. # More complex tests e = ('*', ('+, 1, 2), ('-', 3, 4)) e2 = ('*', e, ('+', 5, 6)) f = ('+', ('-', ('+', ('*', ("*', 1, 3), 5), ('*', ('*', 1, 3), 6)), ('+', ("*', ('*', 1, 4), 5), ('*', ("*', 1, 4), 6))), ('-', ('+', ("*', ('*', 2, 3), 5), ('*', ("*', 2, 3), 6)), ('+', ("*', ("*', 2, 4), 5), ('*', ("*', 2, 4), 6)))) applied_distributivity(apply_distributive(e2), f) e = ('*', ('*', ('+', 1, 2), ('-', 3, 4)), ('*', ('-', 5, 6), ('+', 7, 8))) f = ('+', ('-', ('+', ('*', (*', 1, 3), ('*', 5, 7)), (**', ("*', 1, 3), (**', 5, 8))), ('+', ('*', ('*', 1, 3), ('*', 6, 7)), (**', ('*', 1, 3), ('*', 6, 8)))), ('-', ('+', ("*', ('*', 1, 4), ('*', 5, 7)), ('*', ('*', 1, 4), ('*', 5, 8))), ('+', ("*', ('*', 1, 4), ('*', 6, 7)), ('*', ("*', 1, 4), ('*', 6, 8))))), ('-', ('-', ('+', ('*', ('*', 2, 3), ('*', 5, 7)), (**', ('*', 2, 3), ('*', 5, 8))), ('+', ("*', ("*', 2, 3), ('*', 6, 7)), (**', ("*', 2, 3), ('*', 6, 8)))), ('-', ('+', ("*', (**', 2, 4), ('*', 5, 7)), ("*', ("*', 2, 4), ("*', 5, 8))), ('+', ("*', ("*', 2, 4), ('*', 6, 7)), (**', ("*', 2, 4), ('*', 6, 8)))))) applied_distributivity (apply_distributive(e), f) Challenge Question Question 9: Distributive property If you truly want to test your teeth on a difficult recursion, here is grist for your teeth. This question is worth just a few points, so that students can score well even without doing it. But if you are starving for a difficult question, here is one. This is difficult. Attempt at your own risk. Instructor is not responsible for the many hours you may end up spending on this problem. Please, do not ask for help about this question in office hours; let people who are doing the regular questions benefit from office hour time. Implement the apply_distributive_property function, which applies the distributive property to an expression to push down multiplication to the leaves as far as possible. The function should apply, recursively, the following transformations: f(g+h) = fgfh (f+g)h = fh Egh until the multiplications cannot be moved down further in the expression tree. Hint: If you have e = ej Oe2, you first must apply distributivity to ej and ez, obtaining e' and eq. If 0 + *, then you can just return e Oes. If 0 = *, then you must consider whether e orely has the form 91 +92. Assume el, does. This means your expression is e{ *(91 +92), and you need to apply distributivity: e{*(91 +92) =(e *91)+(@{ *92) The trick is that fter you apply distributivity obtain (@{ *91)+(e* 92), you must again apply distributivity to both (*g), (e *92) obtaining f1, f2, respectively. This step is necessary because (e *91) now has * as top operator, and you may need to "push it down" using distributivity, obtaining fi; similarly for (@{ *92). Finally, you can return f1 + f2. [] ### Exercise: Implement apply_distributive def apply_distributive(e): ""Applies the distributive property to an expression e.""" ### YOUR CODE HERE [] ### Simple test for distributivity. 2 points. ## Here is a definition of equality that disregards order. def is distributed (exp): def is_plusminus(exp): return isinstance(exp, tuple) and exp[@] in '+-' if isinstance(exp, tuple): op, e1, e2 = exp if op == '*' and (is_plusminus(el) or is_plusminus(e2)): return False return is_distributed (01) and is_distributed(e2) import random #def value_equality(ei, e2): #return True def applied_distributivity(f, g): return is_distributed(g) and value_equality(f, g) # Simple test e = ('*', ('+', 1, 2), ('-', 3, 4)) f = ('+', ('-', ("*', 1, 3), ("*', 1, 4)), ('-', ("*', 2, 3), ("*', 2, 4))) applied_distributivity(apply_distributive(e), f) [] ### More complicated tests for distributivity. 2 points. # More complex tests e = ('*', ('+, 1, 2), ('-', 3, 4)) e2 = ('*', e, ('+', 5, 6)) f = ('+', ('-', ('+', ('*', ("*', 1, 3), 5), ('*', ('*', 1, 3), 6)), ('+', ("*', ('*', 1, 4), 5), ('*', ("*', 1, 4), 6))), ('-', ('+', ("*', ('*', 2, 3), 5), ('*', ("*', 2, 3), 6)), ('+', ("*', ("*', 2, 4), 5), ('*', ("*', 2, 4), 6)))) applied_distributivity(apply_distributive(e2), f) e = ('*', ('*', ('+', 1, 2), ('-', 3, 4)), ('*', ('-', 5, 6), ('+', 7, 8))) f = ('+', ('-', ('+', ('*', (*', 1, 3), ('*', 5, 7)), (**', ("*', 1, 3), (**', 5, 8))), ('+', ('*', ('*', 1, 3), ('*', 6, 7)), (**', ('*', 1, 3), ('*', 6, 8)))), ('-', ('+', ("*', ('*', 1, 4), ('*', 5, 7)), ('*', ('*', 1, 4), ('*', 5, 8))), ('+', ("*', ('*', 1, 4), ('*', 6, 7)), ('*', ("*', 1, 4), ('*', 6, 8))))), ('-', ('-', ('+', ('*', ('*', 2, 3), ('*', 5, 7)), (**', ('*', 2, 3), ('*', 5, 8))), ('+', ("*', ("*', 2, 3), ('*', 6, 7)), (**', ("*', 2, 3), ('*', 6, 8)))), ('-', ('+', ("*', (**', 2, 4), ('*', 5, 7)), ("*', ("*', 2, 4), ("*', 5, 8))), ('+', ("*', ("*', 2, 4), ('*', 6, 7)), (**', ("*', 2, 4), ('*', 6, 8)))))) applied_distributivity (apply_distributive(e), f)









