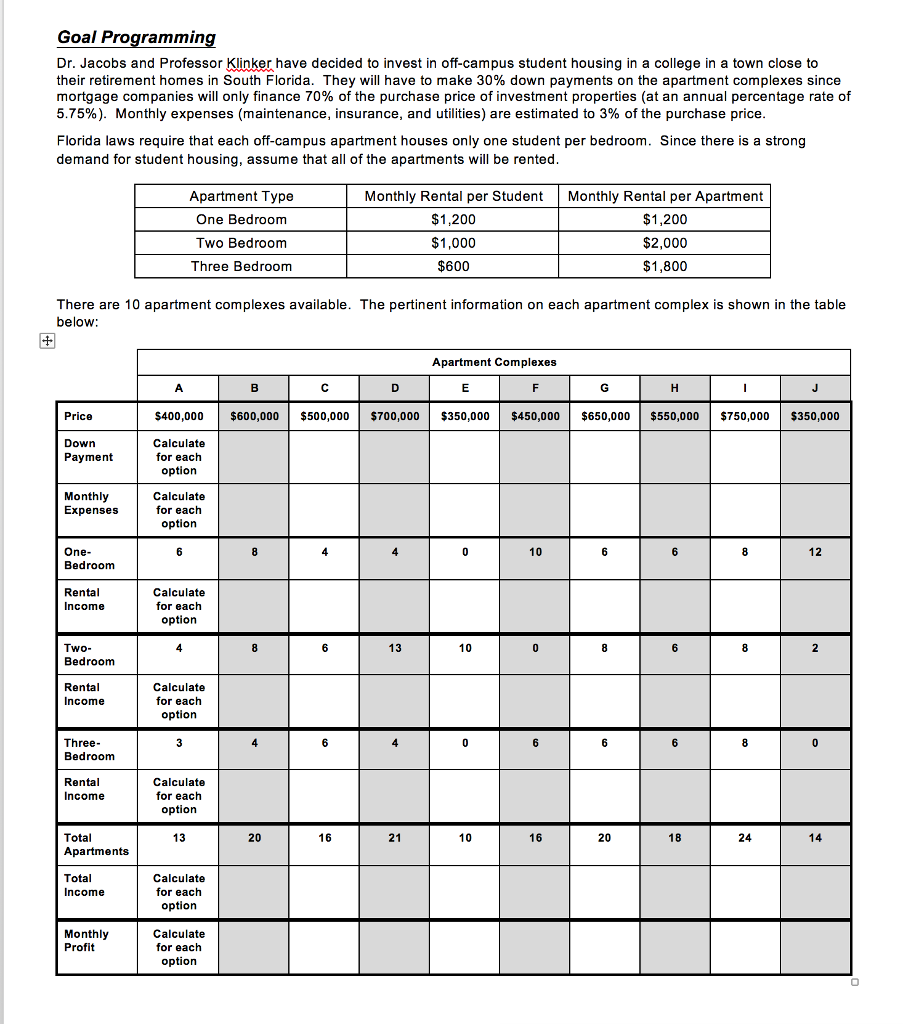
Dr. Jacobs and Professor Klinker have the following constraints that cannot be violated.

The total monthly rent from the one-bedroom apartments cannot exceed 45% of the total monthly rent.

The total monthly rent from the two-bedroom apartments cannot exceed 40% of the total monthly rent.

The total monthly rent from the three-bedroom apartments cannot exceed 35% of the total monthly rent.

The total number of apartments cannot exceed 120.

Dr. Jacobs and Professor Klinker ran a linear program with binary decision variables (1 for Buy, 0 for Dont Buy) There was an optimal solution that would satisfy all of their constraints simultaneously with all decision variables for the apartment complexes being binary.

After researching the rental market near the college and surveying the present students, Dr. Jacobs and Professor Klinker have established the following goals that they want to incorporate into their model:

Goal 1: The total of the down payments cannot exceed $1,600,000.

Goal 2: No less than 30 one-bedroom apartments.

Goal 3: No more than 55 one-bedroom apartments.

Goal 4: No less than 25 two-bedroom apartments.

Goal 5: No more than 50 two-bedroom apartments.

Goal 6: No more than 30 three-bedroom apartments.

Goal 7: Total monthly profit is at least $25,000.

However, when they added the constraints for the 7 goals into their linear program, the problem may be infeasible

Dr. Jacobs and Professor Kinker have the following constraints that cannot be violated. The total monthly rent from the one-bedroom apartments cannot exceed 45% of the total monthly rent. The total monthly rent from the two-bedroom apartments cannot exceed 40% of the total monthly rent. The total monthly rent from the three-bedroom apartments cannot exceed 35% of the total monthly rent. The total number of apartments cannot exceed 120. Dr. Jacobs and Professor Klinker ran a linear program with binary decision variables (1 for "Buy", 0 for "Don't Buy") There was an optimal solution that would satisfy all of their constraints simultaneously with all decision variables for the apartment complexes being binary. After researching the rental market near the college and surveying the present students, Dr. Jacobs and Professor Klinker have established the following goals that they want to incorporate into their model: Goal 1: The total of the down payments cannot exceed $1,600,000 Goal 2: No less than 30 one-bedroom apartments Goal 3: No more than 55 one-bedroom apartments Goal 4: No less than 25 two-bedroom apartments Goal 5: No more than 50 two-bedroom apartments Goal 6: No more than 30 three-bedroom apartments. Goal 7: Total monthly profit is at least $25,000. However, when they added the constraints for the 7 goals into their linear program, the problem may be infeasible. Dr. Jacobs and Professor Kinker have the following constraints that cannot be violated. The total monthly rent from the one-bedroom apartments cannot exceed 45% of the total monthly rent. The total monthly rent from the two-bedroom apartments cannot exceed 40% of the total monthly rent. The total monthly rent from the three-bedroom apartments cannot exceed 35% of the total monthly rent. The total number of apartments cannot exceed 120. Dr. Jacobs and Professor Klinker ran a linear program with binary decision variables (1 for "Buy", 0 for "Don't Buy") There was an optimal solution that would satisfy all of their constraints simultaneously with all decision variables for the apartment complexes being binary. After researching the rental market near the college and surveying the present students, Dr. Jacobs and Professor Klinker have established the following goals that they want to incorporate into their model: Goal 1: The total of the down payments cannot exceed $1,600,000 Goal 2: No less than 30 one-bedroom apartments Goal 3: No more than 55 one-bedroom apartments Goal 4: No less than 25 two-bedroom apartments Goal 5: No more than 50 two-bedroom apartments Goal 6: No more than 30 three-bedroom apartments. Goal 7: Total monthly profit is at least $25,000. However, when they added the constraints for the 7 goals into their linear program, the problem may be infeasible