Question
Draughts (also known as checkers) is a game played on an mm grid of squares, alternately colored light and dark. (The game is usually played
Draughts (also known as checkers) is a game played on an mm grid of squares, alternately colored light and dark. (The game is usually played on an 8 8 or 10 10 board, but the rules easily generalize to any board size.) Each dark square is occupied by at most one game piece (usually called a checker in the U.S.), which is either black or white; light squares are always empty. One player (White) moves the white pieces; the other (Black) moves the black pieces. Consider the following simple version of the game, essentially American checkers or British draughts, but where every piece is a king. Pieces can be moved in any of the four diagonal directions, either one or two steps at a time. On each turn, a player either moves one of her pieces one step diagonally into an empty square, or makes a series of jumps with one of her checkers. In a single jump, a piece moves to an empty square two steps away in any diagonal direction, but only if the intermediate square is occupied by a piece of the opposite color; this enemy piece is captured and immediately removed from the board. Multiple jumps are allowed in a single turn as long as they are made by the same piece. A player wins if her opponent has no pieces left on the board. Describe an algorithm that correctly determines whether White can capture every black piece, thereby winning the game, in a single turn. The input consists of the width of the board (m), a list of positions of white pieces, and a list of positions of black pieces. For full credit, your algorithm should run in O(n) time, where n is the total number of pieces. [Hint: The greedy strategymake arbitrary jumps until you get stuckdoes not always find a winning sequence of jumps even when one exists. See problem ??. Parity, parity, parity.]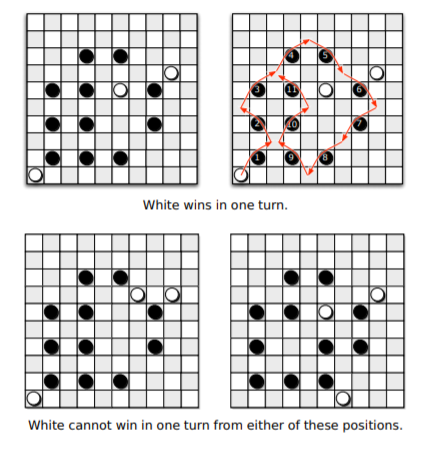
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


