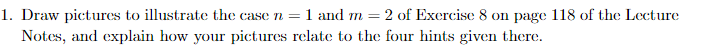Draw pictures to illustrate the case n = 1 and m = 2 of Exercise 8 on page 118 of the Lecture Notes, and explain how your pictures relate to the four hints given there.
Question:
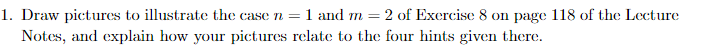
Exercise 8 on page 118:

= 1. Draw pictures to illustrate the case n = 1 and m 2 of Exercise 8 on page 118 of the Lecture Notes, and explain how your pictures relate to the four hints given there. 119 3. EXTREMAL PROBLEMS AND LAGRANGE MULTIPLIERS (2,4, 2) satisfying 1 X1 + X920, -X1 +2,2y, 2 3 , 1 = 1 = - = = I = 2 7 = -- +2 (+ 5 V 29 +3(1= 29 V 29 3 = -y + 2, z+y for some choice of 11 and 12. The third equation gives li = 3 and then the first two equations give and y Then the fifth equation gives 1 = + = and hence 19 = **. Thus z = 7 and y = = and finally the fourth equation shows that z=1-x+y=1= 79. The corresponding values of f at these two points are f(x,y,z) = = +2= = 3 = 29. The maximum value off on the curve of intersection is thus 3 + V29, and occurs at the constrained critical point (1+ EXERCISE 8. Let g: 3m mbe C1, let 3 be the level set g = c, and let f:3*+m- 3 be C4. Follow the hints below to prove that if f restricted to 3 has a local extreme value at p. and if the gradients {9; (p)}=1 are linearly independent, where 9; are the components of g, then Vf (p) Span{ 91 (P), 792 (P),..., 59 (p)}. (1) The m x (n + m) matrix Dg (p) has rank m, and by permuting variables we may suppose that the final m columns of Dg (p) are linearly indepen- dent. Now write the variable in Enum as (x,y) ER" x Rm and set p= (a, b). Apply the Implicit Function Theorem to obtain a locally de fined c function h:U-3 for some open set U in 2" that contains a, and such that 3 is given locally as the graph of h. (2) Then with the graph parameterization H x) = (x,h (x)), we conclude that go H equals the constant vector c near a, and that fo H has a local (unconstrained) extreme value at a. Thus by the chain rule and Fermat's theorem, we have (2.4) Onxn D (9-H) (a) = Dg (p) DH(a), 01xn D(foH) a = Df (p) DH(a), where the matrices Dg (p), DH (a) and Df (p) have size respectively m x (n + m), (n + m) xn, and 1 x (n + m). (3) The top n rows of DH a) are the standard unit vectors en....er in R". Thus DH a) has rank n and so its n columns are linearly independent in R*+Furthermore, the m rows of Dg (p) are linearly independent in R*m, and by the first line in (2.4), each of these rows is perpendicular to each of the columns in DH (a). (4) Thus the m rows of Dg (p) form a basis of the linear space of vectors perpendicular to the n columns of DH a) (why is this?). The second line in (2.4) shows that the row vector Df(p) lies in this linear space, which is the desired conclusion. = = 1. Draw pictures to illustrate the case n = 1 and m 2 of Exercise 8 on page 118 of the Lecture Notes, and explain how your pictures relate to the four hints given there. 119 3. EXTREMAL PROBLEMS AND LAGRANGE MULTIPLIERS (2,4, 2) satisfying 1 X1 + X920, -X1 +2,2y, 2 3 , 1 = 1 = - = = I = 2 7 = -- +2 (+ 5 V 29 +3(1= 29 V 29 3 = -y + 2, z+y for some choice of 11 and 12. The third equation gives li = 3 and then the first two equations give and y Then the fifth equation gives 1 = + = and hence 19 = **. Thus z = 7 and y = = and finally the fourth equation shows that z=1-x+y=1= 79. The corresponding values of f at these two points are f(x,y,z) = = +2= = 3 = 29. The maximum value off on the curve of intersection is thus 3 + V29, and occurs at the constrained critical point (1+ EXERCISE 8. Let g: 3m mbe C1, let 3 be the level set g = c, and let f:3*+m- 3 be C4. Follow the hints below to prove that if f restricted to 3 has a local extreme value at p. and if the gradients {9; (p)}=1 are linearly independent, where 9; are the components of g, then Vf (p) Span{ 91 (P), 792 (P),..., 59 (p)}. (1) The m x (n + m) matrix Dg (p) has rank m, and by permuting variables we may suppose that the final m columns of Dg (p) are linearly indepen- dent. Now write the variable in Enum as (x,y) ER" x Rm and set p= (a, b). Apply the Implicit Function Theorem to obtain a locally de fined c function h:U-3 for some open set U in 2" that contains a, and such that 3 is given locally as the graph of h. (2) Then with the graph parameterization H x) = (x,h (x)), we conclude that go H equals the constant vector c near a, and that fo H has a local (unconstrained) extreme value at a. Thus by the chain rule and Fermat's theorem, we have (2.4) Onxn D (9-H) (a) = Dg (p) DH(a), 01xn D(foH) a = Df (p) DH(a), where the matrices Dg (p), DH (a) and Df (p) have size respectively m x (n + m), (n + m) xn, and 1 x (n + m). (3) The top n rows of DH a) are the standard unit vectors en....er in R". Thus DH a) has rank n and so its n columns are linearly independent in R*+Furthermore, the m rows of Dg (p) are linearly independent in R*m, and by the first line in (2.4), each of these rows is perpendicular to each of the columns in DH (a). (4) Thus the m rows of Dg (p) form a basis of the linear space of vectors perpendicular to the n columns of DH a) (why is this?). The second line in (2.4) shows that the row vector Df(p) lies in this linear space, which is the desired conclusion. =