Drawing Trees on a grid. When drawing trees on a grid, each node must be assigned an x- and y-coordinate. Edges are then drawn between a node and its children. For binary trees, there is a simple and elegant way of assigning nodes their coordinates so that the resulting drawing is nice. For each node v, let its x-coordinate be i if v is the ith node processed by an inorder traversal of the tree; let its y-coordinate be -j if the depth of v in the tree is j. The binary tree below is drawn using the said x- and y-coordinates. For example, r has coordinates (12; 0), d has coordinates (10;-2) while s has coordinates (17;-4).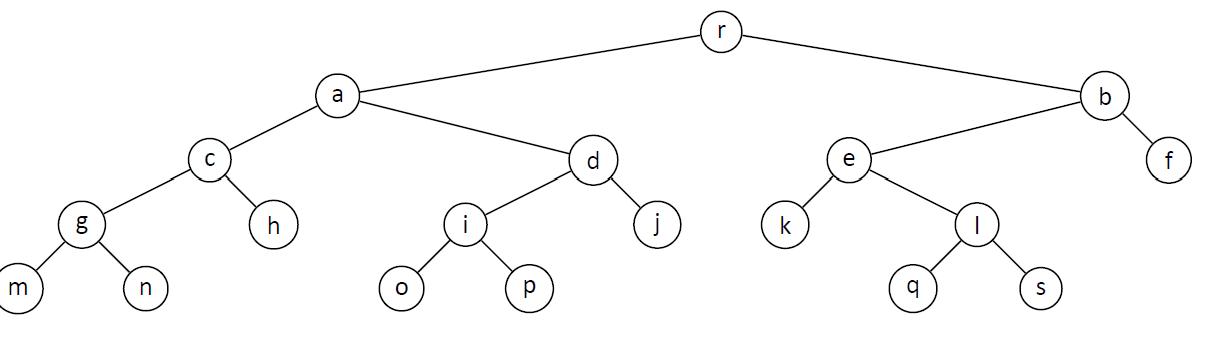 The above technique though does not generalize to arbitrary trees in order traversals are only meaningful on binary trees. So we need to design a more flexible algorithm. But first, lets clarify what it means for a grid drawing of a tree to be nice. For the rest of the problem, assume that references to the children of each node v is stored in v.children. The children are also ordered that is, there is a first child, a second child, etc. and the children are accessed in the said order. Lastly, assume that every node has an even number of children, like quadtrees or octrees, etc. Here are the rules: Each node is assigned integer x- and y-coordinates. Two nodes that have the same depth in T are assigned the same y-coordinate.

When node v has 2k children, the first k children and their subtrees have x-coordinates smaller than vs x-coordinate while the second set of k chlldren and their subtrees have x-coordinates larger than vs x-coordinate.

Q1. Given a tree T with n nodes, design an O(n)-time algorithm that assigns each node x- and y-coordinates that obey the three rules above. The x-coordinates must range from 1 to n while the y-coordinates range from h to 0, where h is the height of T. Your output should consist of n print statements of the form Draw v.label at (x-coordinate, y- coordinate). Reminder: Every node in the tree has an even number of nodes. The number of children though may vary from node to node (e.g., one node may have 2 children, another 4 children, etc.)

Q2. What extra rule would you suggest for drawing trees where the nodes can have an odd number of children? Why?

m m