DSP First Lab 1 (Chapters 2 and 3) handoutThis is an individual lab report which will be graded by answering each of the following questions. Please submit a MATLAB script (.m file) that will do each of the following. Please be sure to heavily comment each portion of your code. 1. (30 points) Sampling and plotting sinusoids The signals we use in the real world, such as our voices, are called analog signals. To process these signals in computers, we need to convert the signals to digital form. While an analog signal is continuous in both time and amplitude, a digital signal is discrete in both time and amplitude. To convert a signal from continuous time to discrete time, a process called sampling is used. The value of the signal is measured at certain intervals in time. Conversely, if we actually want to plot a continuous signal using MATLAB which can only work with discrete signals represented by row or column vectors, then we must evaluate that continuous signal at a discrete set of times. Usually we pick a uniform set , where n is an integer and is called the sample spacing or sampling =period. Then a continuous signal can be converted to a discrete signal .()()Now given a continuous signal , please plot the 3 digital signals in ()=20cos (2(30)0.3)one figure at using a blue solid line, using a red star symbol (*), and 1=0.0052=0.00253 using a green dashed line. Please display three periods and add legends for each signal =0.0005with their specific .2. (20 points) Adding two sinusoids with the same frequency We now consider an example of adding two sinusoids , 3()=1()+2()where and . 1()=1.7cos (20+70/180)2()=1.9cos (20+200/180)Please use the subplot function to plot the real parts of the 3 signals in one graphical space with 3 rows by 1 column (31), add a title to each subgraph.3. (20 points) Plot spectrum of sinusoids (bar, instead of stem plot please)The following MATLAB code defines a vector zz, which corresponds to the signal z(t): tt = -10:0.01:10; %time is in seconds kk=2;zz = kk*cos(kk*tt); kk=4; zz = zz + kk*cos(kk*tt - pi/3); kk=6; zz = zz + real(2*exp(j*pi/4)*exp(j*kk*tt)); a) Write a formula for z(t) in terms of sinusoids in standard form, that is, z(t)= A0 + k Akcos(kt +k). (5 points)
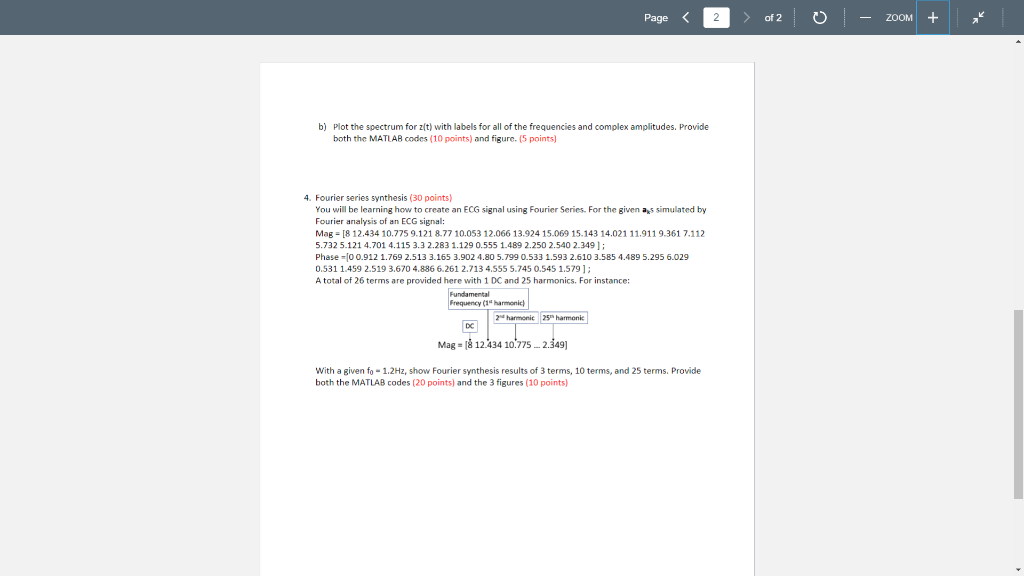
b) Plot the spectrum for z(t) with labels for all of the frequencies and complex amplitudes. Provide both the MATLAB codes (10 points) and figure. (5 points) 4. Fourier series synthesis (30 points)You will be learning how to create an ECG signal using Fourier Series. For the given aks simulated by Fourier analysis of an ECG signal:Mag = [8 12.434 10.775 9.121 8.77 10.053 12.066 13.924 15.069 15.143 14.021 11.911 9.361 7.112 5.732 5.121 4.701 4.115 3.3 2.283 1.129 0.555 1.489 2.250 2.540 2.349 ] ;Phase =[0 0.912 1.769 2.513 3.165 3.902 4.80 5.799 0.533 1.593 2.610 3.585 4.489 5.295 6.029 0.531 1.459 2.519 3.670 4.886 6.261 2.713 4.555 5.745 0.545 1.579 ] ;A total of 26 terms are provided here with 1 DC and 25 harmonics. For instance:With a given f0 = 1.2Hz, show Fourier synthesis results of 3 terms, 10 terms, and 25 terms. Provide both the MATLAB codes (20 points) and the 3 figures (10 points) b) Plot the spectrum for z(t) with labels for all of the frequencies and complex amplitudes. Provide both the MATLAB codes (10 points) and figure. (5 points) 4. Fourier series synthesis (30 points)You will be learning how to create an ECG signal using Fourier Series. For the given aks simulated by Fourier analysis of an ECG signal:Mag = [8 12.434 10.775 9.121 8.77 10.053 12.066 13.924 15.069 15.143 14.021 11.911 9.361 7.112 5.732 5.121 4.701 4.115 3.3 2.283 1.129 0.555 1.489 2.250 2.540 2.349 ] ;Phase =[0 0.912 1.769 2.513 3.165 3.902 4.80 5.799 0.533 1.593 2.610 3.585 4.489 5.295 6.029 0.531 1.459 2.519 3.670 4.886 6.261 2.713 4.555 5.745 0.545 1.579 ] ;A total of 26 terms are provided here with 1 DC and 25 harmonics. For instance:With a given f0 = 1.2Hz, show Fourier synthesis results of 3 terms, 10 terms, and 25 terms. Provide both the MATLAB codes (20 points) and the 3 figures (10 points)
Page 1 of 2 ZOOM + DSP First Lab 1 (Chapters 2 and 3) handout This is an individual lab report which will be graded by answering each of the following questions. Please submit a MATLAB script (.m file) that will do each of the following, Please be sure to heavily comment each portion of your code. 1. (30 points) Sampling and plotting sinusoids The signals we use in the real world, such as our voices, are called "analog" signals. To process these signals in computers, we need to convert the signals to "digital" form. While an analog signal is continuous in both time and amplitude, a digital signal is discrete in both time and amplitude. To convert a signal from continuous time to discrete time, a process called sampling is used. The value of the signal is measured at certain intervals in time. Conversely, if we actually want to plota continuous signal using MATLAB which can only work with discrete signals represented by row or column vectors, then we must evaluate that continuous signal at a discrete set of times. Usually we pick a uniform sett, nt, where n is an integer and T, is called the sample spacing or sampling period. Then a continuous signal X(t) can be converted to a discrete signal x(nt.). Now given a continuous signal X(t) = 20cos (2(30)t - 0.31), please plot the 3 digital signals in one figure at T.1 -0.005s using a blue solid line, T.2 -0.0025s using a red star symbol (*), and 78 -0.0005s using a green dashed line. Please display three periods and add legends for each signal with their specific T. 2. (20 points) Adding two sinusoids with the same frequency We now consider an example of adding two sinusoids X3(t) = x1(0) + X(t). where x:(t) - 1.7cos (20xt + 70/180) and x2(t) - 1.9cos (20nt + 200/180). Please use the subplot function to plot the real parts of the 3 signals in one graphical space with 3 rows by 1 column (3x1), add a title to each subgraph. 3. (20 points) Plot spectrum of sinusoids (bar, instead of stem plot please) The following MATLAB code defines a vector 22, which corresponds to the signal z(t): zz = kkcos (kk tt); zz - zz + kk*cos(kk*tt - pi/3); kk-63 zz = zz + real (2*exp("pi/4) *exp("kk*tt)): a) Write a formula for z(t) in terms of sinusoids in standard form, that is, (t)= A + XA contp.). (5 points) Page of 2 ZOOM + b) Plot the spectrum for z(t) with labels for all of the frequencies and complex amplitudes. Provide both the MATLAB codes (10 points) and figure. (5 points) 4. Fourier series synthesis (30 points) You will be learning how to create an ECG signal using Fourier Series. For the given as simulated by Fourier analysis of an ECG signal: Mag = [8 12,434 10.775 9.121 8.77 10.053 12.066 13.924 15.069 15.143 14.021 11.911 9.361 7.112 5.732 5.121 4.701 4.115 3.3 2.283 1.129 0.555 1.489 2.250 2.540 2.349); Phase [0 0.912 1.769 2.513 3.165 3.902 4.80 5.799 0.533 1.593 2.610 3.585 4.489 5.295 6.029 0.531 1.459 2.519 3.670 4.8866.261 2.713 4.555 5.745 0.545 1.579]; A total of 26 terms are provided here with 1 DC and 25 harmonics. For instance: Fundamental Frequency (1" harmonic 2e harmonic 25 harmonie DC Mag = 18 12.434 10775...2.349) With a given to - 1.2Hz, show Fourier synthesis results of 3 terms, 10 terms, and 25 terms. Provide both the MATLAB codes (20 points) and the 3 figures (10 points) Page 1 of 2 ZOOM + DSP First Lab 1 (Chapters 2 and 3) handout This is an individual lab report which will be graded by answering each of the following questions. Please submit a MATLAB script (.m file) that will do each of the following, Please be sure to heavily comment each portion of your code. 1. (30 points) Sampling and plotting sinusoids The signals we use in the real world, such as our voices, are called "analog" signals. To process these signals in computers, we need to convert the signals to "digital" form. While an analog signal is continuous in both time and amplitude, a digital signal is discrete in both time and amplitude. To convert a signal from continuous time to discrete time, a process called sampling is used. The value of the signal is measured at certain intervals in time. Conversely, if we actually want to plota continuous signal using MATLAB which can only work with discrete signals represented by row or column vectors, then we must evaluate that continuous signal at a discrete set of times. Usually we pick a uniform sett, nt, where n is an integer and T, is called the sample spacing or sampling period. Then a continuous signal X(t) can be converted to a discrete signal x(nt.). Now given a continuous signal X(t) = 20cos (2(30)t - 0.31), please plot the 3 digital signals in one figure at T.1 -0.005s using a blue solid line, T.2 -0.0025s using a red star symbol (*), and 78 -0.0005s using a green dashed line. Please display three periods and add legends for each signal with their specific T. 2. (20 points) Adding two sinusoids with the same frequency We now consider an example of adding two sinusoids X3(t) = x1(0) + X(t). where x:(t) - 1.7cos (20xt + 70/180) and x2(t) - 1.9cos (20nt + 200/180). Please use the subplot function to plot the real parts of the 3 signals in one graphical space with 3 rows by 1 column (3x1), add a title to each subgraph. 3. (20 points) Plot spectrum of sinusoids (bar, instead of stem plot please) The following MATLAB code defines a vector 22, which corresponds to the signal z(t): zz = kkcos (kk tt); zz - zz + kk*cos(kk*tt - pi/3); kk-63 zz = zz + real (2*exp("pi/4) *exp("kk*tt)): a) Write a formula for z(t) in terms of sinusoids in standard form, that is, (t)= A + XA contp.). (5 points) Page of 2 ZOOM + b) Plot the spectrum for z(t) with labels for all of the frequencies and complex amplitudes. Provide both the MATLAB codes (10 points) and figure. (5 points) 4. Fourier series synthesis (30 points) You will be learning how to create an ECG signal using Fourier Series. For the given as simulated by Fourier analysis of an ECG signal: Mag = [8 12,434 10.775 9.121 8.77 10.053 12.066 13.924 15.069 15.143 14.021 11.911 9.361 7.112 5.732 5.121 4.701 4.115 3.3 2.283 1.129 0.555 1.489 2.250 2.540 2.349); Phase [0 0.912 1.769 2.513 3.165 3.902 4.80 5.799 0.533 1.593 2.610 3.585 4.489 5.295 6.029 0.531 1.459 2.519 3.670 4.8866.261 2.713 4.555 5.745 0.545 1.579]; A total of 26 terms are provided here with 1 DC and 25 harmonics. For instance: Fundamental Frequency (1" harmonic 2e harmonic 25 harmonie DC Mag = 18 12.434 10775...2.349) With a given to - 1.2Hz, show Fourier synthesis results of 3 terms, 10 terms, and 25 terms. Provide both the MATLAB codes (20 points) and the 3 figures (10 points)








