Each question below specifies a graph operation, a graph representation, and a desired bound. The possible answers are all O() or () complexity measures written in terms of V (the number of vertices in the graph) and/or E (the number of edges in the graph).

All graphs are directed, unweighted graphs.

You are to choose the complexity measure that correctly characterizes the desired bound on the provided operation, assuming that the specified representation is being used.

If more than one complexity measure is correct, choose the one that is tightest.

Keep these two things in mind:

• When determining best cases, do not assume that V = E = 0, or anything of the sort. Instead, imagine what graph with V vertices and E edges would lead to the lowest running time.
• Do not assume that the number of edges entering or leaving a vertex is stored explicitly.
• Assume that an adjacency list is an array of linked lists, and that the linked lists are not ordered in any particular way

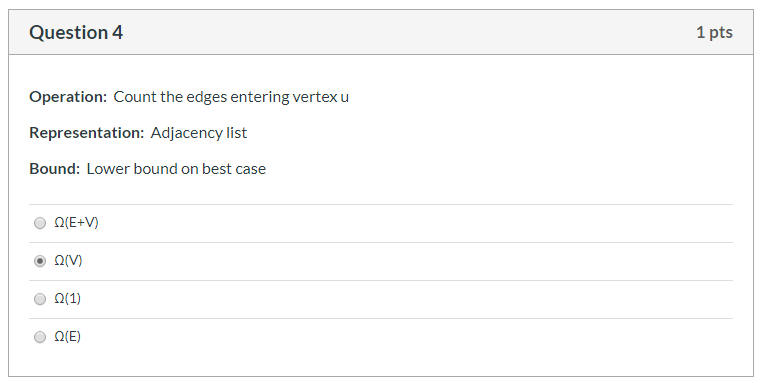
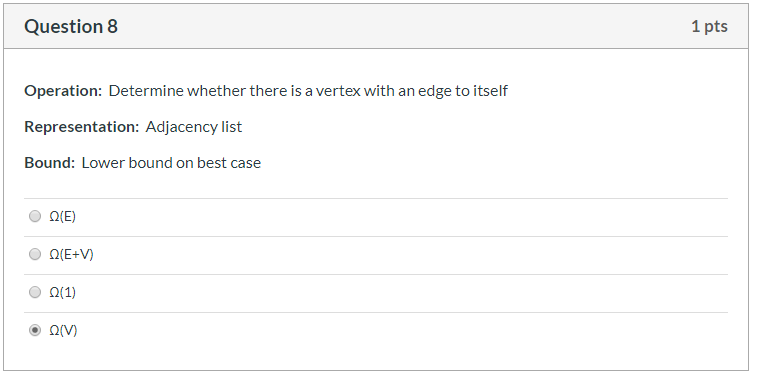
Question 4 1 pts Operation: Count the edges entering vertex u Representation: Adjacency list Bound: Lower bound on best case Q(E+V) Q(V) O 0(1) Q(E) Question 8 1 pts Operation: Determine whether there is a vertex with an edge to itself Representation: Adjacency list Bound: Lower bound on best case Q(E) O QE+V) O 0(1) O Q(V) Question 14 1 pts Operation: Determine whether every vertex has exactly two edges out Representation: Adjacency matrix Bound: Lower bound on best case Q(E) O 01V2 011) (E+V)