Each screenshot includes multiple parts. As so, please do all parts, or else I will have to give you a thumbs down. I need all parts or I cannot do anything! Thanks.

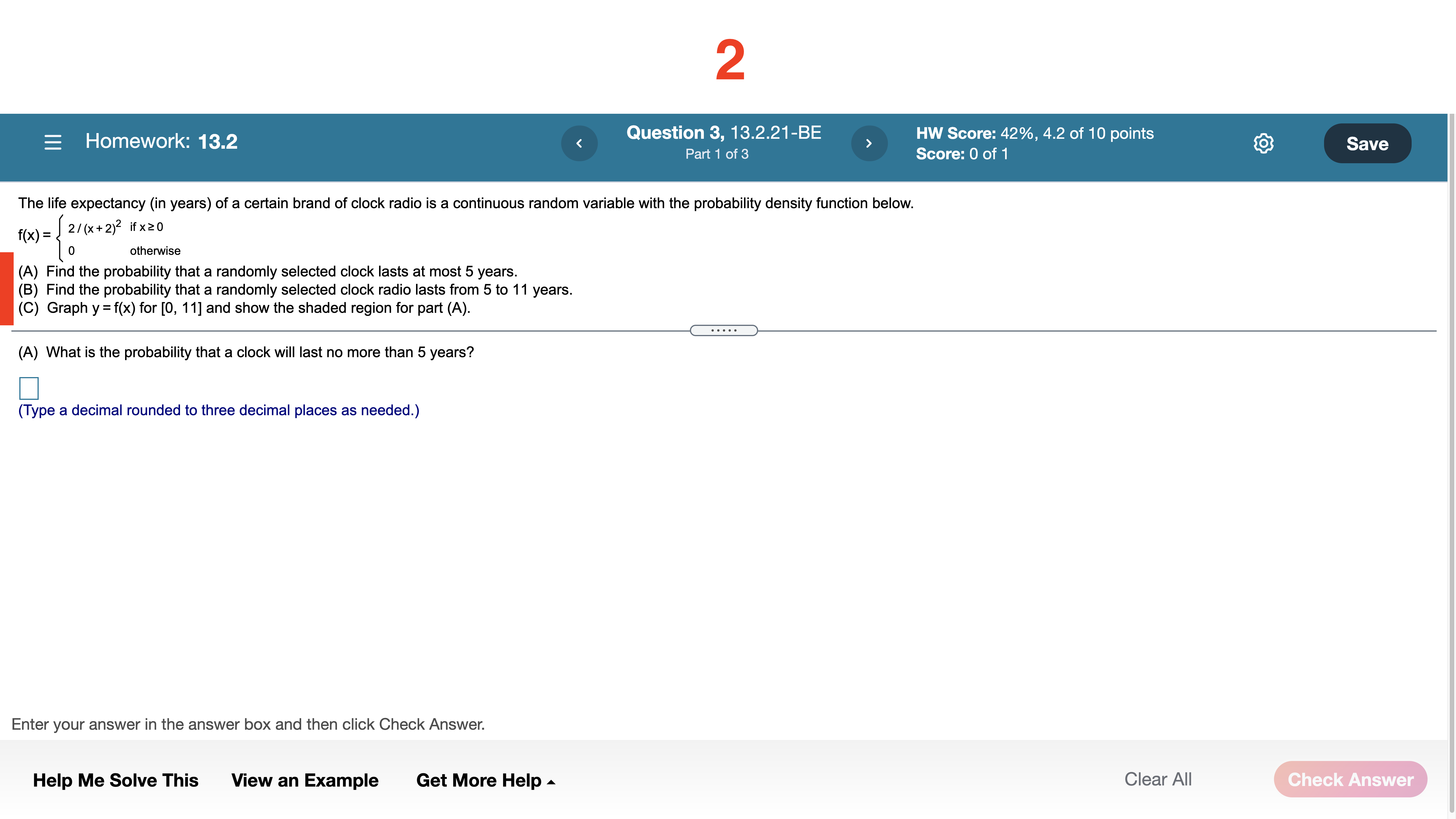
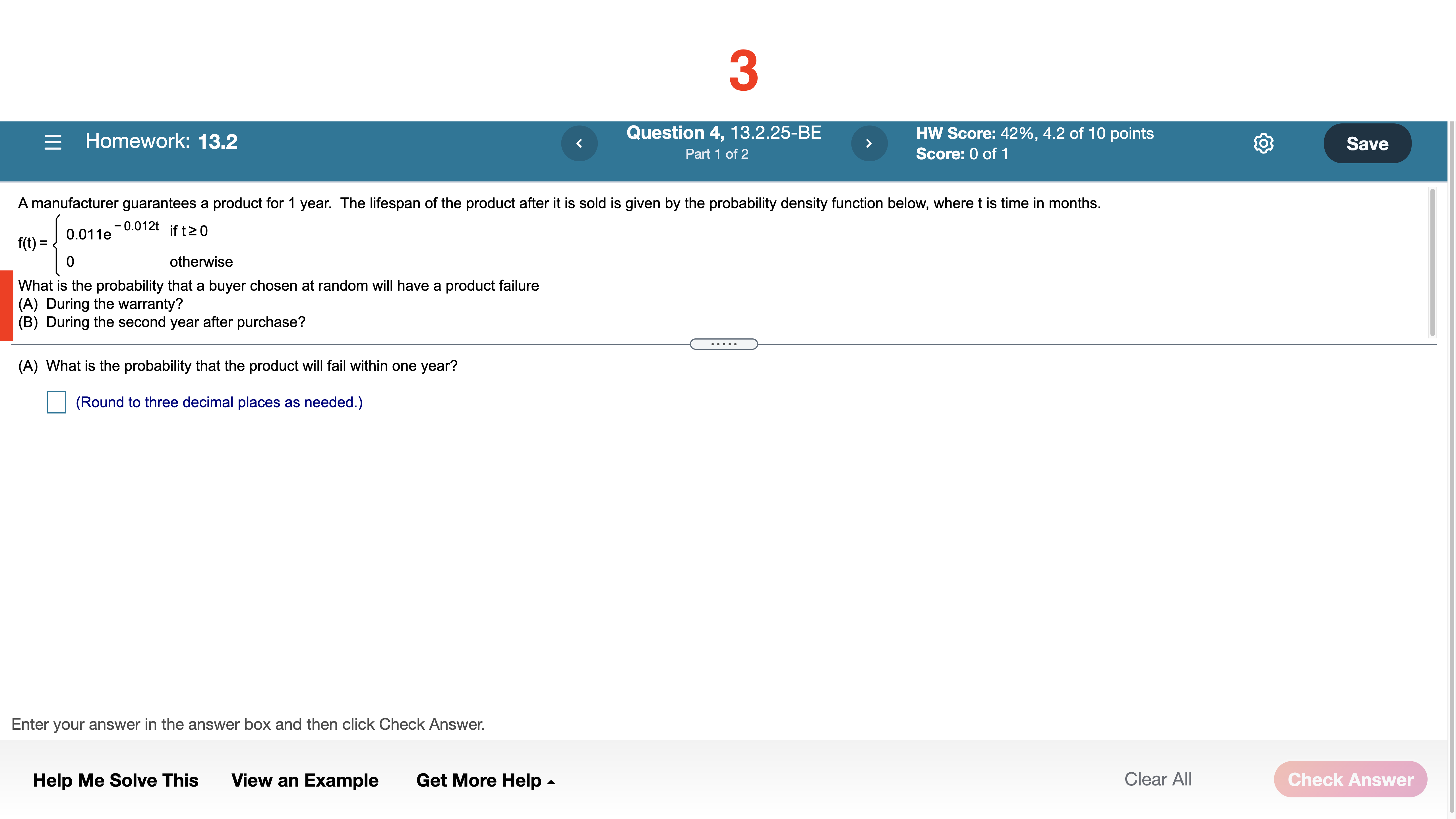
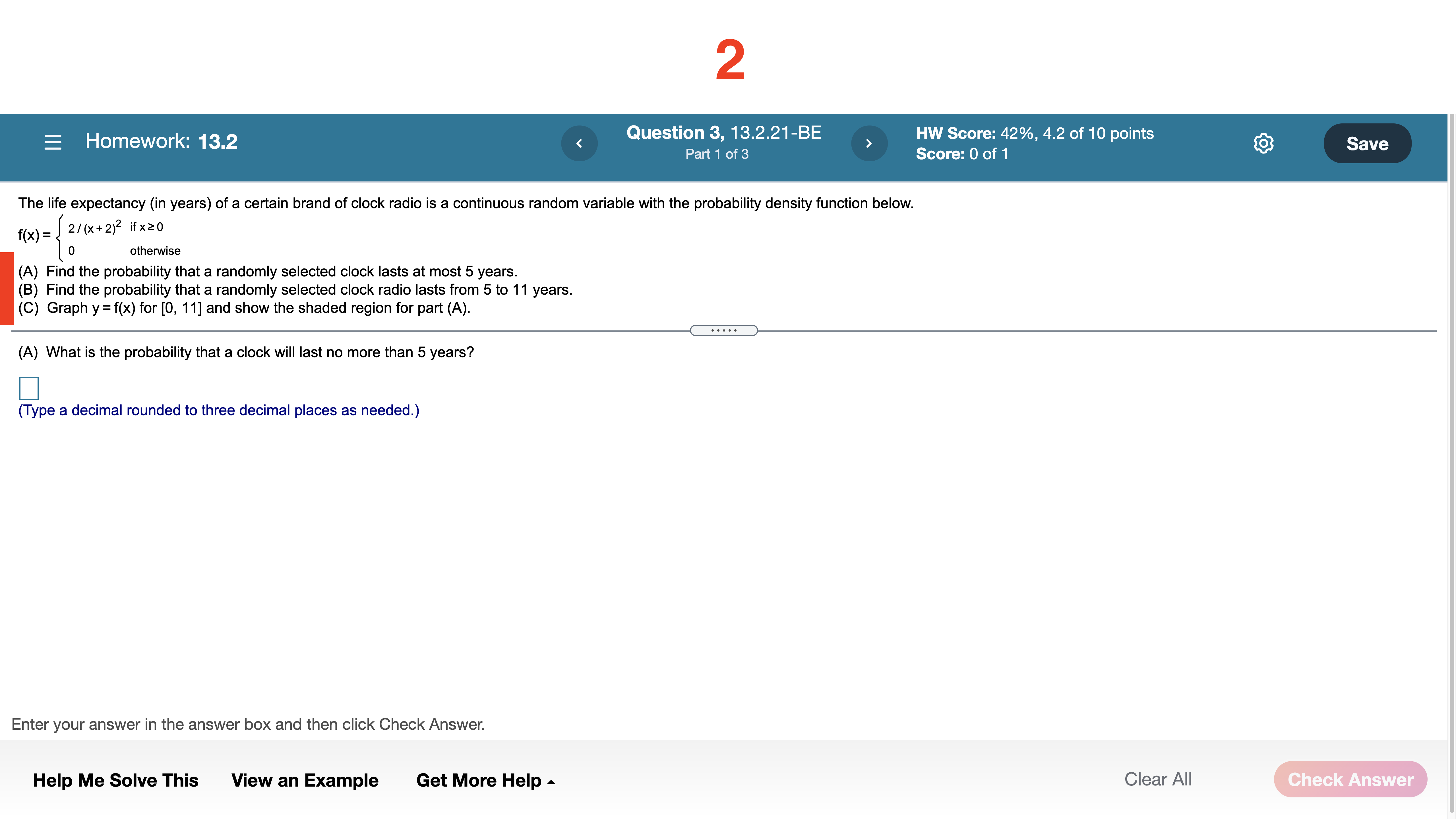
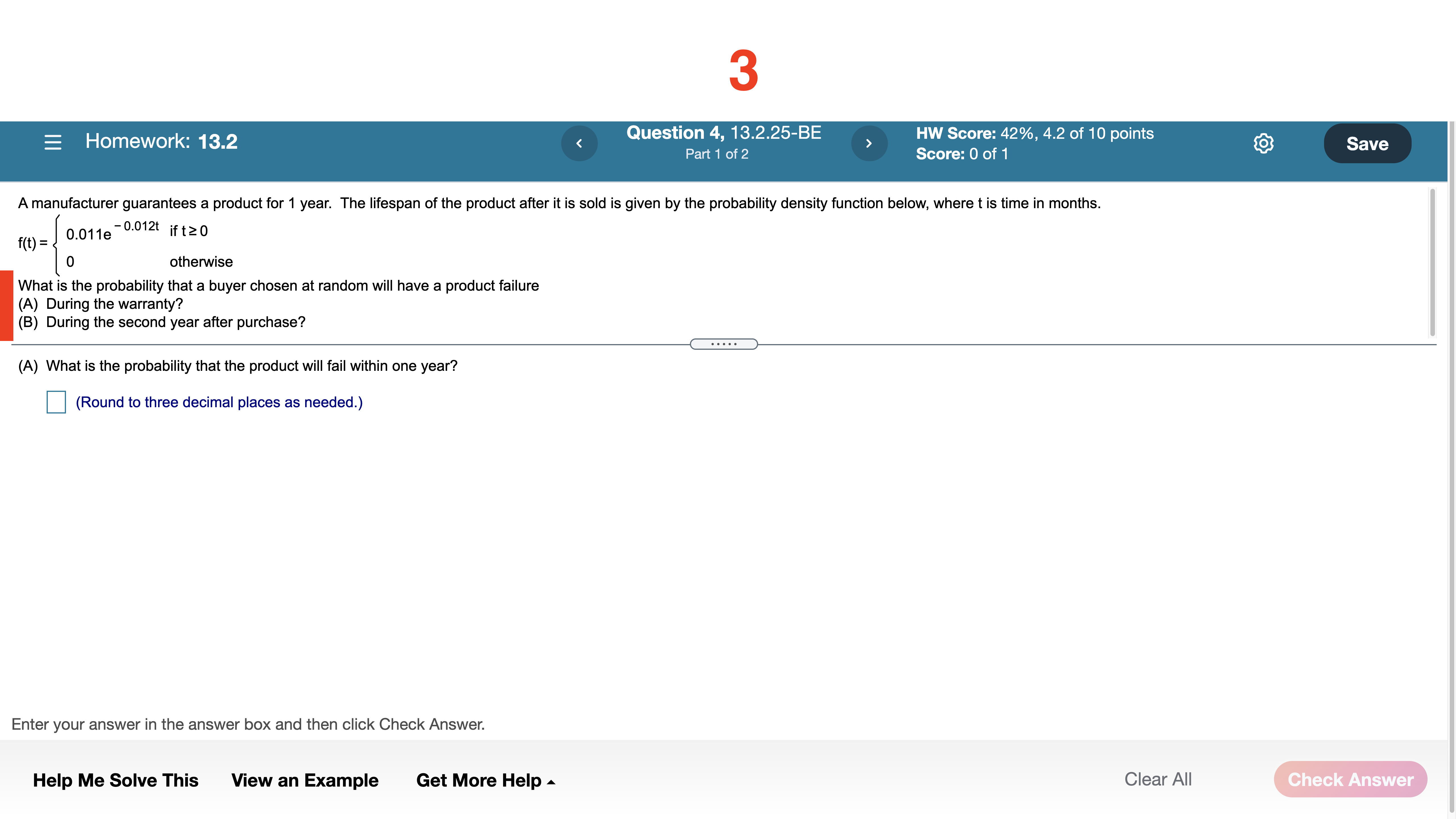
Question 10, 12.5.89-LS HW Score: 70%, 7 of 10 points Part1 of 2 ' Score: 0 of 1 E Homework: 12.5 Ayeast culture weighing 2 grams is removed from a refrigerator unit and is expected to grow at the rate of W'(t) = 0.2 e 0'2' grams per hour at a higher controlled temperature. How much will the weight of the culture increase during the rst 10 hours of growth? How much will the weight of the culture increase from the end of the 10th hour to the end of the 20th hour of growth? The weight increase during the rst 10 hours is approximately grams. (Type an integer or decimal rounded to three decimal places as needed.) part 2, highlighted in \"how much will the weight . . .\" Enter your answer in the answer box and then click Check Answer. Help Me Solve This View an Example Get More Help A Clear All Homework; 132 Question 3, 13.2.21-BE > HW Score: 42%, 4.2 of 10 points Part 1 of 3 Score: 0 of 1 The life expectancy (in years) of a certain brand of clock radio is a continuous random variable with the probability density function below. f(x) = 2/(x+2)2 itsz 0 atheMisa (A) Find the probability that a randomly selected clock lasts at most 5 years. (B) Find the probability that a randomly selected clock radio lasts from 5 to 11 years. (C) Graph y =f(x) for [0, 11] and show the shaded region for part (A). (A) What is the probability that a clock will last no more than 5 years? (Type a decimal rounded to three decimal places as needed.) Enter your answer in the answer box and then click Check Answer. Help Me Solve This View an Example Get More Help A Clear All Question 4, 13.2.25-BE > HW Score: 42%, 4.2 of 10 points Part 1 of 2 Score: 0 of 1 Homework: 13.2 A manufacturer guarantees a product for 1 year. The lifespan of the product after it is sold is given by the probability density function below, where t is time in months. -o.o1zr \"a 0 f(t)= 0.011e I 0 othenNise What is the probability that a buyer chosen at random will have a product failure (A) During the warranty? (B) During the second year after purchase? (A) What is the probability that the product will fail within one year? (Round to three decimal places as needed.) Enter your answer in the answer box and then click Check Answer. Help Me Solve This View an Example Get More Help A Clear All