ECLIPSE:

Here is the last homework code:

TestArithmetic.java

import java.util.Random;

public class TestArithmetic { static Random random = new Random(); public static void main(String[] args) { for (int i = 0; i

Node.java

public class Node { /** * Constructor */ public Node() { } /** * @return the evaluated value of this node */ public double eval() { System.out.println("Error: eval Node"); return 0; } }

Binop.java

public class Binop extends Node { protected Node lChild, rChild;

/** * @param l * @param r */ public Binop(Node l, Node r) { lChild = l; rChild = r; } }

Divide.java

public class Divide extends Binop {

public Divide(Node l, Node r) { super(l, r); }

public double eval() { return lChild.eval() / rChild.eval(); } public String toString() { return "(" + lChild.toString() + " / " + rChild.toString() + ")"; } }

Minus.java

public class Minus extends Binop { public Minus(Node l, Node r) { super(l, r); } public double eval() { return lChild.eval() - rChild.eval(); } public String toString() { return "(" + lChild.toString() + " - " + rChild.toString() + ")"; }

}

Mult.java

public class Mult extends Binop {

public Mult(Node l, Node r) { super(l, r); }

public double eval() { return lChild.eval() * rChild.eval(); } public String toString() { return "(" + lChild.toString() + " * " + rChild.toString() + ")"; } }

Const.java

public class Const extends Node { private double value; /** * Constructor to initialize the constant value for operation * * @param d constant value */ public Const(double d) { value = d; } public double eval() { return value; } public String toString() { return "" + value; } }

Plus.java

public class Plus extends Binop { public Plus(Node l, Node r) { super(l, r); } public double eval() { return lChild.eval() + rChild.eval(); } public String toString() { return "(" + lChild.toString() + " + " + rChild.toString() + ")"; } }

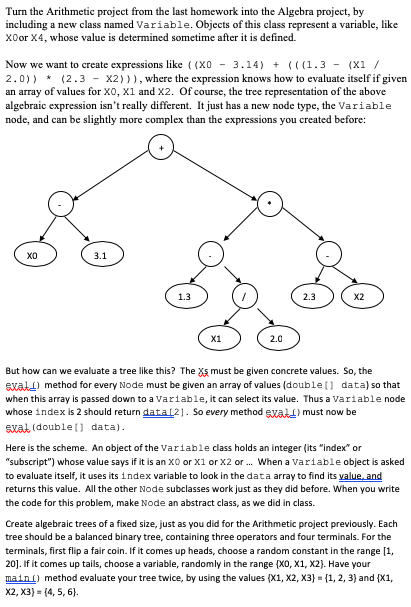
Turn the Arithmetic project from the last homework into the Algebra project, by including a new class named Variable. Objects of this class represent a variable, like XOor X4, whose value is determined sometime after it is defined. Now we want to create expressions like ((xO 3.14)(1.3 (xi/ 2.0)) (2.3-X2))), where the expression knows how to evaluate itself if given an array of values for X0, X1 and X2. Of course, the tree representation of the above algebraic expression isn't really different. It just has a new node type, the Variable node, and can be slightly more complex than the expressions you created before: X0 3.1 1.3 2.3 X2 X1 2.0 But how can we evaluate a tree like this? The s must be given concrete values. So, the exa) method for every Node must be given an array of values (double[ data) so that when this array is passed down to a Variable, it can select its value. Thus a Variable node whose index is 2 should return data21. So every method eva) must now be eval (double data) Here is the scheme. An object of the Variable class holds an integer (its "index or "subscript") whose value says if it is an XO or X1 or X2 or When a Variable object is asked to evaluate itself, it uses its index variable to look in the data array to find its yalue and returns this value. All the other Node subclasses work just as they did before. When you write the code for this problem, make Node an abstract class, as we did in class. Create algebraic trees of a fixed size, just as you did for the Arithmetic project previously. Each tree should be a balanced binary tree, containing three operators and four terminals. For the terminals, first flip a fair coin. If it comes up heads, choose a random constant in the range [1, 20]. If it comes up tails, choose a variable, randomly in the range XO, X1, X2). Have your maini) method evaluate your tree twice, by using the values fX1, X2, X3 1, 2, 3) and [x1, x2, x3) (4, 5, 6)