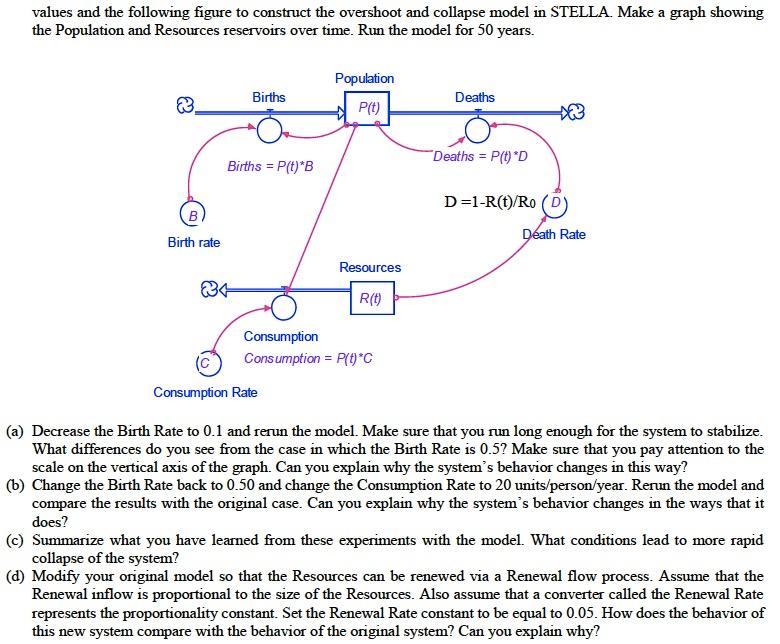
Assume that in the following figure the initial value of Resources is 10,000 units, the initial value of Population is 10 people, the birth rate is 0.50 births/capita/year, and each person consumes two resources units per year. Use these values and the following figure to construct the overshoot and collapse model in STELLA. Make a graph showing the Population and Resources reservoirs over time. Run the model for 50 years. & Birth rate Births = P(t) "B Births = Population P(t) Resources R(t) Consumption Consumption = P(t)*C Deaths "Deaths = P(t) *D D=1-R(t)/Ro -X3 Death Rate Consumption Rate (a) Decrease the Birth Rate to 0.1 and rerun the model. Make sure that you run long enough for the system to stabilize. What differences do you see from the case in which the Birth Rate is 0.5? Make sure that you pay attention to the scale on the vertical axis of the graph. Can you explain why the system's behavior changes in this way? (b) Change the Birth Rate back to 0.50 and change the Consumption Rate to 20 units/person/year. Rerun the model and compare the results with the original case. Can you explain why the system's behavior changes in the ways that it does? (c) Summarize what you have learned from these experiments with the model. What conditions lead to more rapid collapse of the system? (d) Modify your original model so that the Resources can be renewed via a Renewal flow process. Assume that the Renewal inflow is proportional to the size of the Resources. Also assume that a converter called the Renewal Rate represents the proportionality constant. Set the Renewal Rate constant to be equal to 0.05. How does the behavior of this new system compare with the behavior of the original system? Can you explain why?