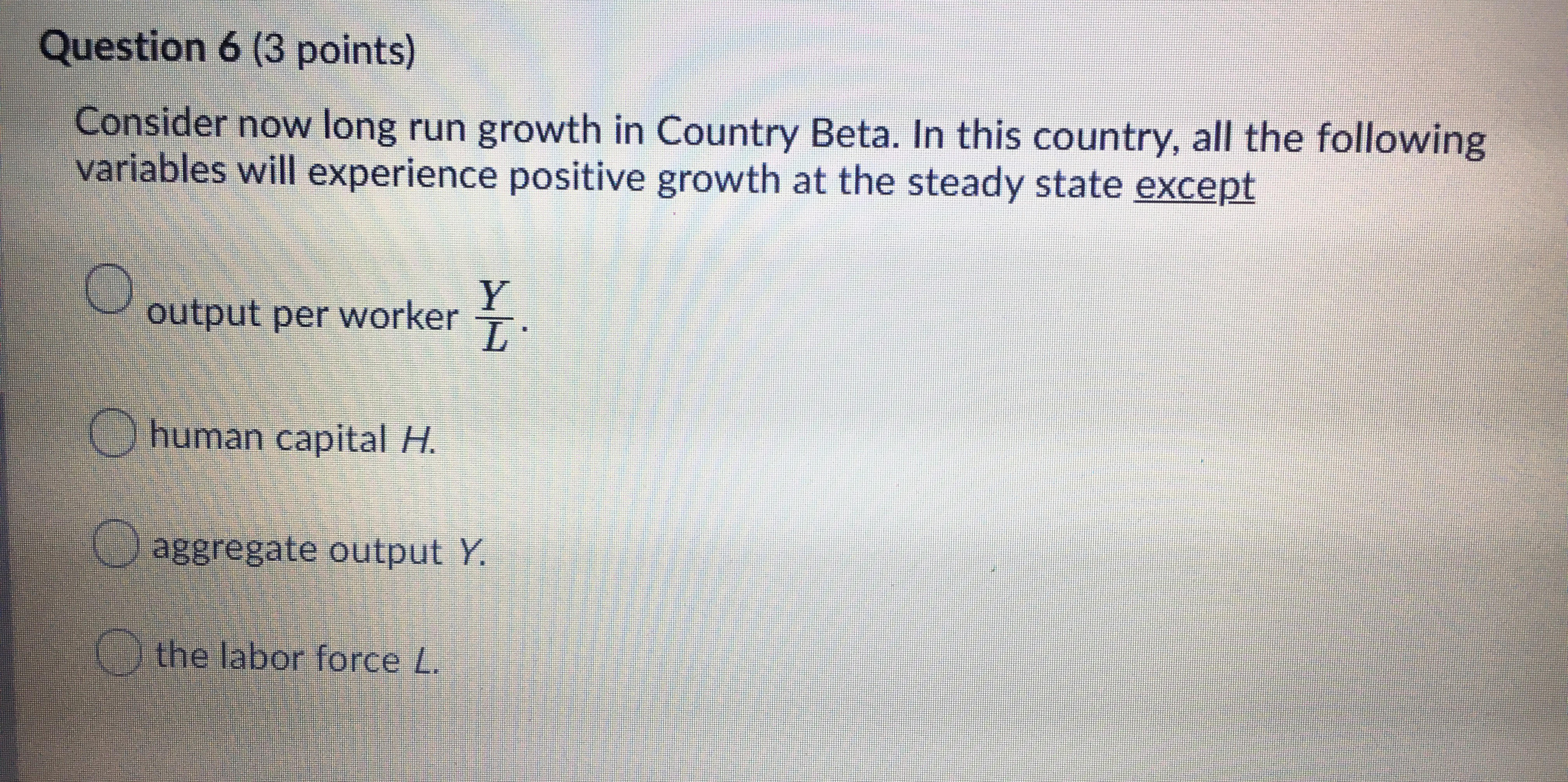
Economics problem

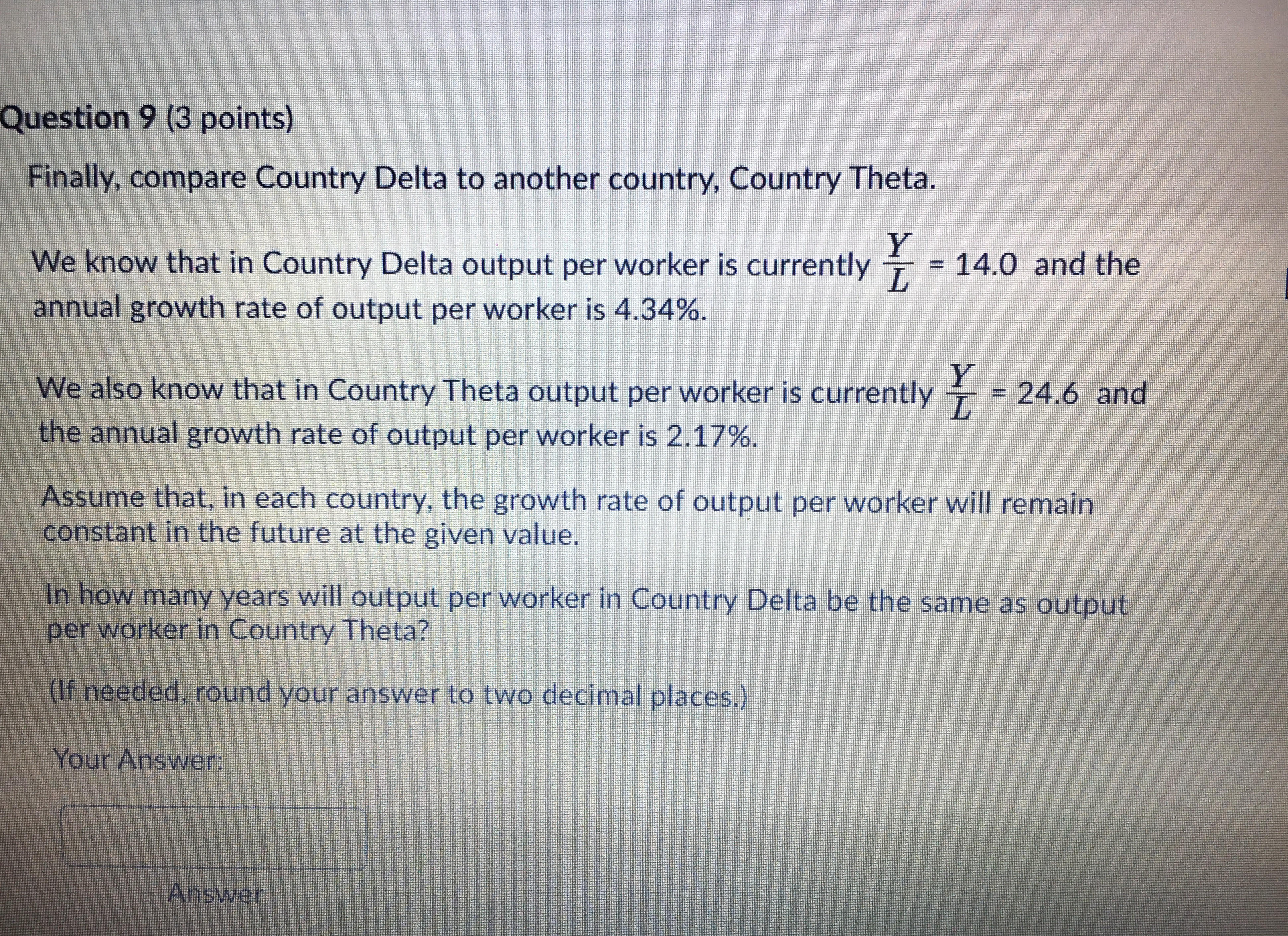
Question 2 (3 points) We know that in Country Alpha the growth rale of the labor force is n = 2.01% and the rate of technological progress is g = 1.37%. Shortly after the increase in the saving rate, we observed that the growth of aggregate output Y in this county was 5.51%. Then, at the same time, the growth rate of output per worker , Y was % (Enter Z% as Z; if needed, round your answer to two decimal places and use the "-" sign if your answer is a negative number.) Your Answer: AnswerQuestion 8 (2.5 points) Consider now long run growth in Country Delta. Which of the following conditions guarantees that aggregate output Y will experience positive growth in this country? The depreciation rate O is larger than the growth rate of the labor force n. The growth rate of the labor force n is positive. The depreciation rate O is smaller than the saving rate s.Question 7 (3 points) Assume that in Country Delta the depreciation rate increases from 0 = 7% to O - 9%. Everything else remains unchanged. As a consequence of this increase in the depreciation rate, the growth rate of output per worker I in Country Delta will O decrease, but only temporarily. increase permanently. O increase, but only temporarily. O remain unchanged. decrease permanently.Question 3 (3 points) In Country Alpha, the increase in the saving rate from s[= 24% to s = 30% will result in a O K temporary increase in the growth rate of capital per worker O permanent increase in the growth rate of capital per worker K I temporary decrease in the growth rate of aggregate capital K. permanent decrease in the growth rate of aggregate capital K.Finally, we are going to examine Country Delta, that operates according to the Endogenous growth model. The production function in Country Delta is: Y = AK where again Y is aggregate output, K is aggregate capital, and A is a parameter. Assume that in Country Delta, A = 1. We know that the labor force L grows at the rate n > 0, capital depreciates at the rate 0 > 0, and the saving rate is s > 0.Question 6 (3 points) Consider now long run growth in Country Beta. In this country, all the following variables will experience positive growth at the steady state except O output per worker L O human capital H. O aggregate output Y. the labor force L.Question 4 (3 points) If aggregate output in Country Beta is currently Y = 1,800 and the number of workers is currently L = 75, then output per worker in this country is equal to (If needed, round your answer to two decimal places.) Your Answer: AnswerWe want now to consider Country Beta, that operates according to the Solow model with human capital. The production function in Country Beta is: Y = Ko H(1-a) where Y is aggregate output, K is aggregate capital, and H = (L X F)eos is human capital. In this last expression, L is the labor force, E is the efficiency of labor, S is the level of education of the labor force, and @ is a parameter. We know that the efficiency of labor E in this country is E = 1 and that it is constant over time (g = 0). In addition, the level of education of the labor force is currently S = 15 (years of schooling) and @ = 0.04 . Finally, we know that the labor force L grows at the rate n > 0. capital depreciates at the rate ( > 0. and the saving rate is s > 0. Assume that Country Beta is currently operating at the steady state of this version of the Solow model.Question 5 (3 points) Assume that in Country Beta the level of education of the labor force increases from S = 15 to S = 16. Everything else remains unchanged. As a consequence of the increase in S, in Country Beta )the growth rate of aggregate output at the steady state will increase. output per worker at the steady state will increase. aggregate output at the steady state will decrease. the growth rate of output per worker at the steady state will increase.In this section we will examine the determinants of long run growth using a few alternative models that we have studied during the course. We will begin with the Solow model. Assume that Country Alpha operates according to the standard version of the Solow model. The production function in Country Alpha is: Y = Ko (L x E) (1-Q) where Y is aggregate output, K is aggregate capital, L is aggregate labor, and E is the efficiency of labor. We know that the efficiency of labor E grows at the rate of technological progress g > 0, the labor force L grows at the rate n > 0, capital depreciates at the rate 0 > 0, and the saving rate is s > 0. Let k = K Y LX E and y = 7 LXE denote capital per effective worker and output per effective worker, respectively. Assume that Country Alpha is currently operating at the steady state of this Solow model.Question 1 (2.5 points) Assume that the authorities of this country implement a series of policy measures that have the result of increasing the saving rate from s = 24% to s = 30%. Everything else in Country Alpha remains unchanged. As a consequence of this increase in the saving rate, the level of capital per effective worker in this country will decrease. increase. remain unchanged.Question 9 (3 points) Finally, compare Country Delta to another country, Country Theta. We know that in Country Delta output per worker is currently - = 14.0 and the annual growth rate of output per worker is 4.34%. We also know that in Country Theta output per worker is currently Y = 24.6 and the annual growth rate of output per worker is 2.17%. Assume that, in each country, the growth rate of output per worker will remain constant in the future at the given value. In how many years will output per worker in Country Delta be the same as output per worker in Country Theta? (If needed, round your answer to two decimal places.) Your