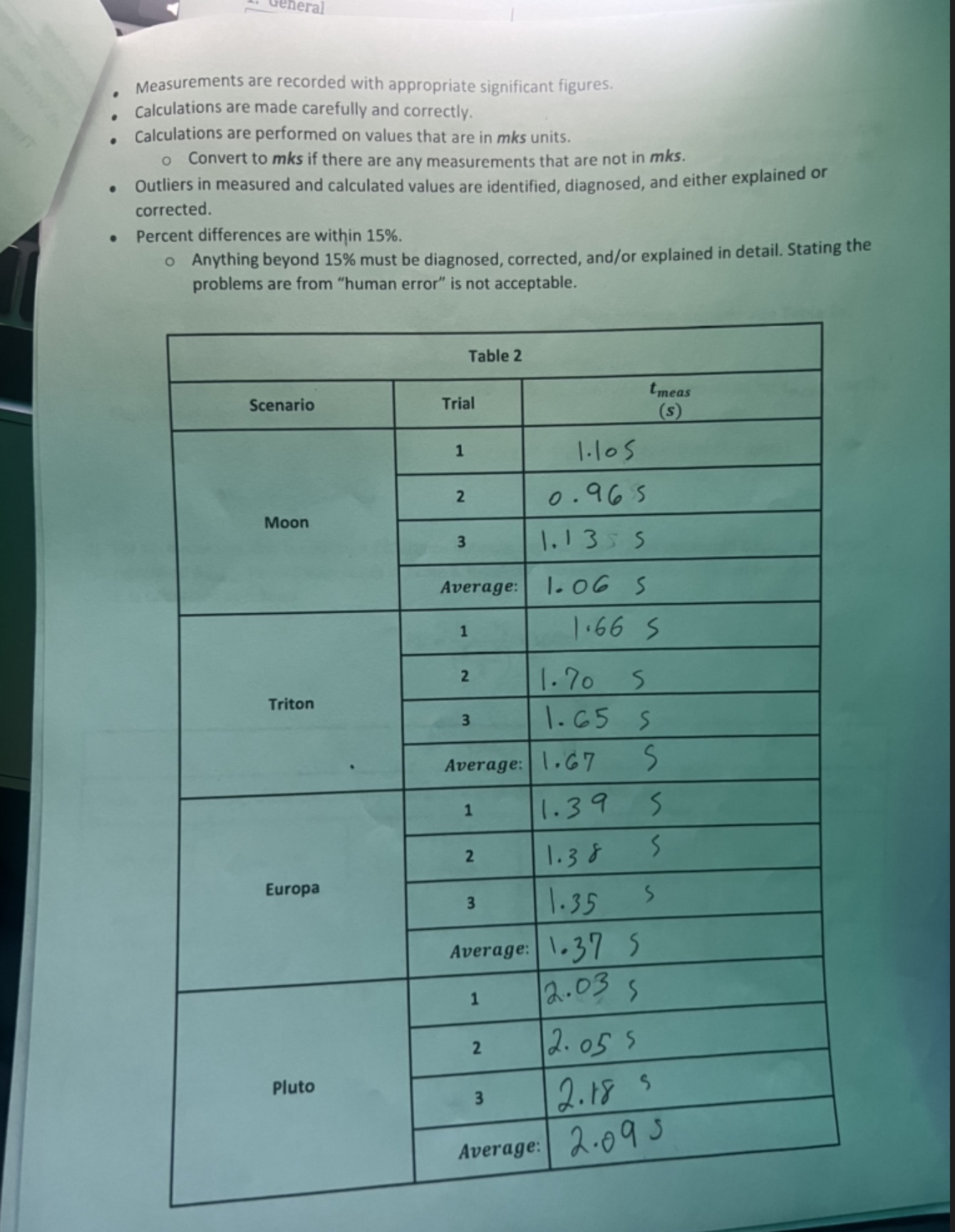
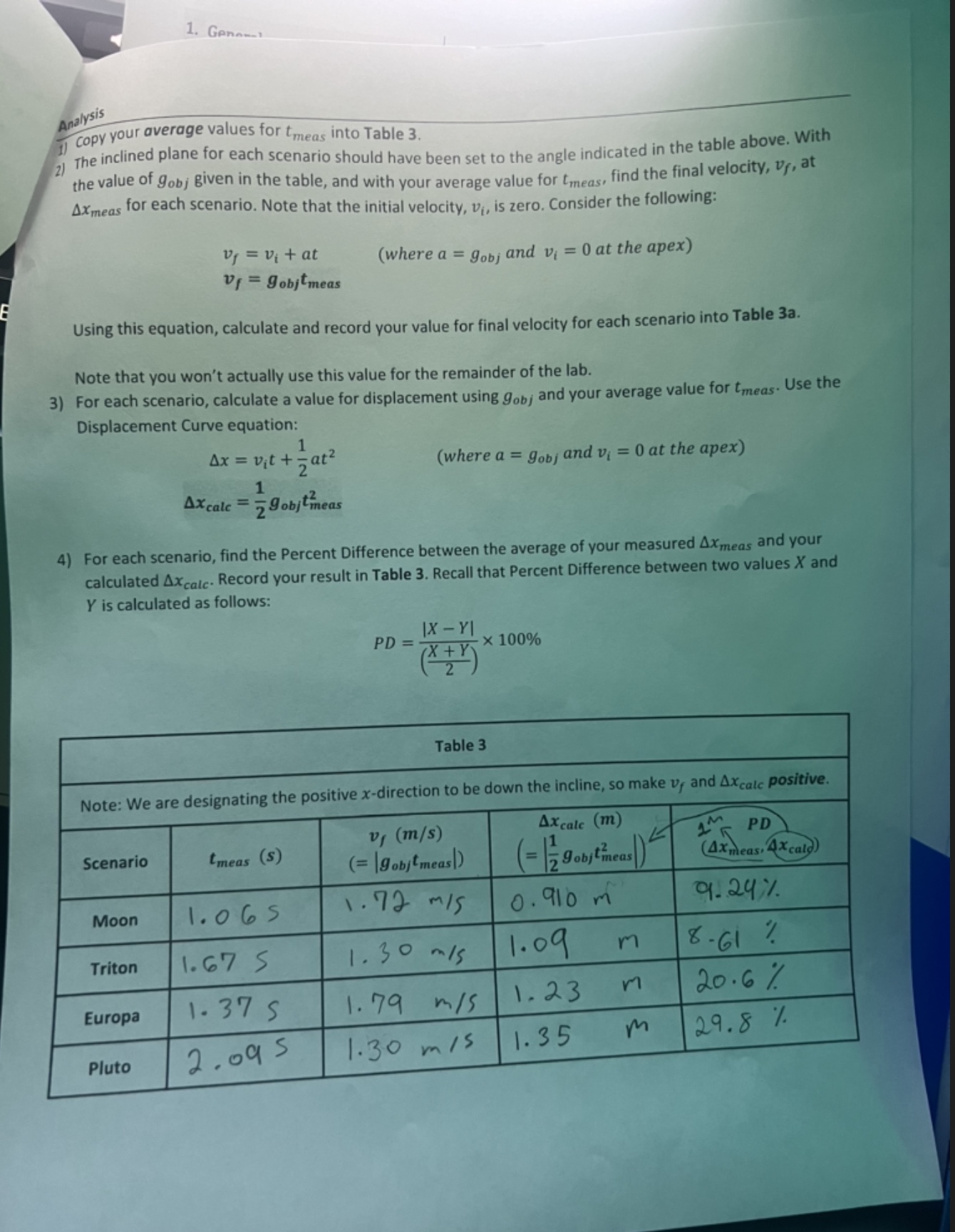
eral . . . Measurements are recorded with appropriate significant figures. Calculations are made carefully and correctly. Calculations are performed on values that are in mks units. o Convert to mks if there are any measurements that are not in mks. Outliers in measured and calculated values are identified, diagnosed, and either explained or corrected. Percent differences are within 15%. o Anything beyond 15% must be diagnosed, corrected, and/or explained in detail. Stating the problems are from "human error" is not acceptable. Table 2 tmeas Scenario Trial (s) 1 1.105 2 0.965 Moon 3 1.1355 Average: 1.06 S 1 1.66 S 2 1.70 S Triton 3 1.65 S Average: 1.67 S 1 1.39 S 2 1.38 S Europa 3 1.35 S Average: 1.37 S 1 12.03s 2 12.055 Pluto 3 2.18 S Average: 2.09 S 1. Gene Analysis 2) The inclined plane for each scenario should have been set to the angle indicated in the table above. With 1) Copy your average values for tmeas into Table 3. the value of gobj given in the table, and with your average value for teas, find the final velocity, vr, at Axmeas for each scenario. Note that the initial velocity, v, is zero. Consider the following: v = v + at vf = gobjtmeas (where a = gobj and v = 0 at the apex) B Using this equation, calculate and record your value for final velocity for each scenario into Table 3a. Note that you won't actually use this value for the remainder of the lab. 3) For each scenario, calculate a value for displacement using gobj Displacement Curve equation: 1 Ax = vit + +at 1 Axcale= gobjmeas and your average value for tmeas. Use the (where a = gobj and v = 0 at the apex) 4) For each scenario, find the Percent Difference between the average of your measured Axmeas and your calculated Axcalc- Record your result in Table 3. Recall that Percent Difference between two values X and Y is calculated as follows: |X - Y\ PD = 100% (X + Y) Table 3 Scenario tmeas (S) v, (m/s) (=9objt meas) Note: We are designating the positive x-direction to be down the incline, so make vy and Axcalc positive. PD Axcale (m) gobjmeas 13 (Axmeas, 4xcale) Moon 1.065 1.72 m/s 0.910 m 9.24% Triton 1.67 5 130 mis 1.09 m 8-61? Europa Pluto 1.37 S 2.095 1.79 m/s 1.23 20.6% 1.30 m/s 1.35 M 29.8% Ma rap b Overview In this lab, you will investigate the motion of an object on an inclined plane. You will use the inclined plane set at various angles as an analog for free-fall on other celestial bodies. There are four scenarios: The Moon. Triton, the largest of Jupiter's Galilean moons. Europa, the smallest of Jupiter's Galilean moons. 3 Pluto, everyone's favorite dwarf planet. A PAScar will slide down various inclines. You will collect data for three runs for each scenario. Each run should be analogous to visiting one of these extraterrestrial bodies, dropping a PAScar from some height, and taking measurements of the time-of-flight. Data Collection 1) Using the procedure described above in Background, complete the gobj/g and obj columns below: Table 1 Object gobj (m/s) gobj/g g= -9.80 m/s obj () (= sin gobj/9) h (m) (= l sin obj) Moon -1.62 0.1653 9.515 Triton -0.779 0.0794 4.55 Europa -1.31 0.1336 7.680 Pluto -0.620 0.0632 3.62 2) Set the angle of the incline, obj, for the first celestial object (starting with the Moon) in accordance with Table 1. a) You can use your choice of methods to set the angle: a smartphone app; a protractor with a plumb bob; or measurements with trigonometry using hand l. 3) Ensure that when the PAScar is positioned near the top of the incline it can roll down 1 meter. 4) One lab partner will release the PAScar at the same time the other lab partner starts the timer. The timer must be stopped as soon as the PAScar has traveled 1 meter. This is the length the car travels down the incline, &, and your "measured" Ax value. 5) Record this time as tmeas in Table 2. Axmeas == 1.00 m 6) After compiling data for three trials of a scenario, calculate average value of tmeas and record your results in Table 2. Repeat steps 2) through 6) for the remainder of the scenarios. Grading Criteria . Instructions are followed. Measurements are made carefully and correctly. Background Many of the problems that are covered in PHY201 involve free-falling objects on Earth, where we assume constant downward acceleration of g = -9.80 m/s. This lab investigates objects sliding down a nearly frictionless inclined plane, where acceleration is some fraction of g. The motion of the object is still in one dimension, but that dimension is along the surface of the inclined plane. It is not perpendicular or parallel to the ground. Consider the following diagrams: a=gsine 6-90-8 B Full gravitational acceleration is g, and it points straight down. However, the acceleration of the object down the incline is a, where a = g sin 8. Note the following edge cases: If the angle is zero (i.e., 0 = 0.00), the plane is horizontal. Because sin 0.00 = 0, the acceleration of the object is zero (a = 0). This is what we expect since objects don't slide down horizontal surfaces. If the angle is perpendicular to the ground (i.e., 90.0), the plane is vertical. Because sin 90.0 = 1, the acceleration of the object is the full acceleration due to gravity (a = g). Again, this is what we expect. There is no surface to impede the fall of the object, so it is truly in free fall. = Now consider an object in free-fall on the surface of the Moon. On its surface, the acceleration due to the Moon's gravity is gmoon = -1.62 m/s. That's 0.165g (i.e., 16.5% of Earth's gravity). Therefore, on Earth, an object sliding down a frictionless inclined plane of some angle moon will fall with the same acceleration as an object in free-fall on the Moon: Starting equation from above: gmoon Solve for moon: Omoon sin-1 = = g sin emoon 9moon g Plug in 0.1653 for 9moon/9: Omoon sin 0.1653 = Omoon = 9.515 an object sliding down a frictionless plane inclined 9.52 above the horizontal will accelerate at the same e as an object in free-fall on the Moon. Wrap-Up Questions 1) What are some possible sources of errors in these scenarios? There are plenty, so list whatever comes to mind. Please be more specific than "human error". 2) The acceleration due to gravity on Neptune is gneptune = -14.07 m/s. If you were to zip up to Neptune and run this inclined plane experiment with the goal of mimicking the acceleration due to gravity on Earth, at what angle would you set the incline? Why can you mimic Earth's gravity on Neptune (using the methods in this lab), but you can't mimic Neptune's gravity on Earth? (Hint: Check out that last little bit in the Background section, above.)