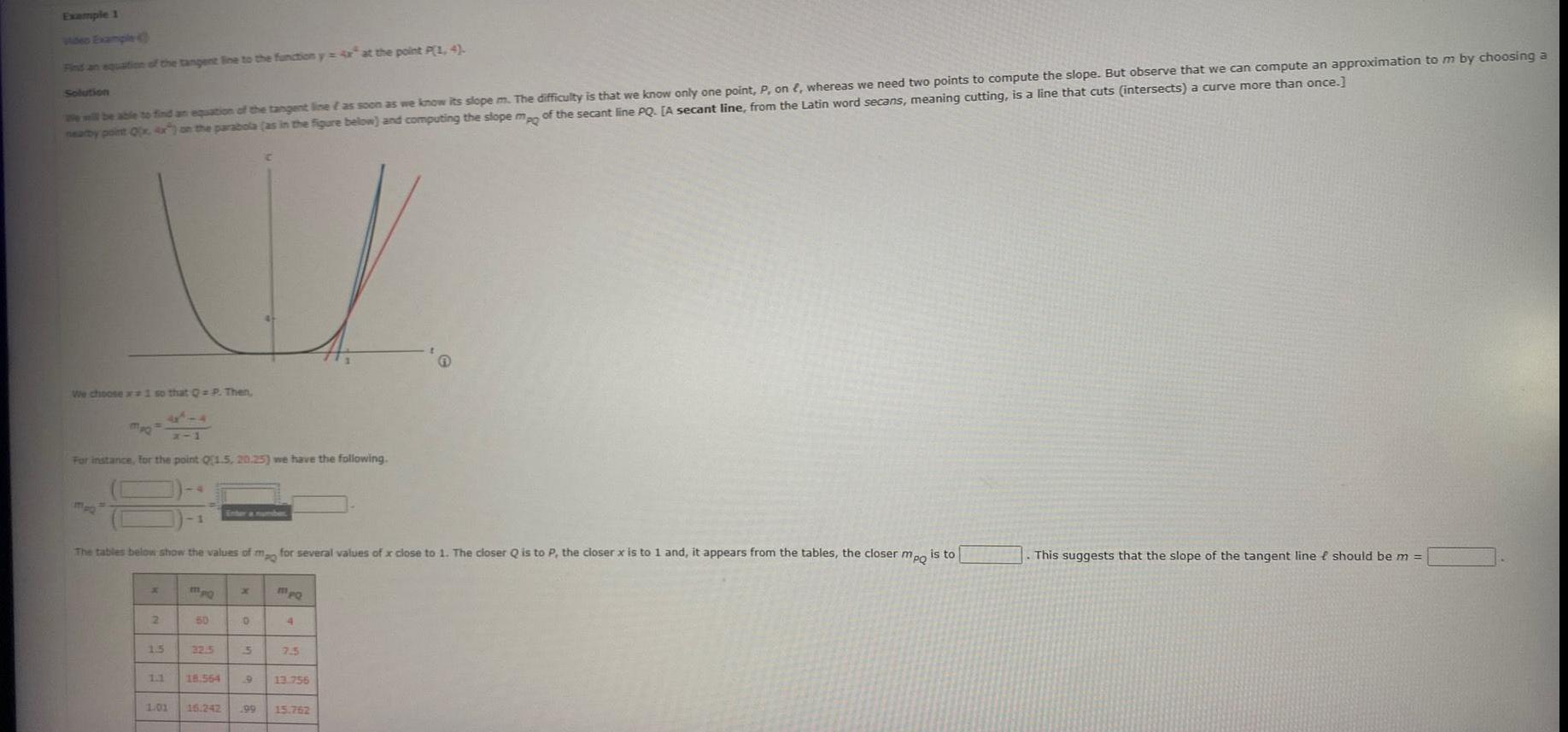
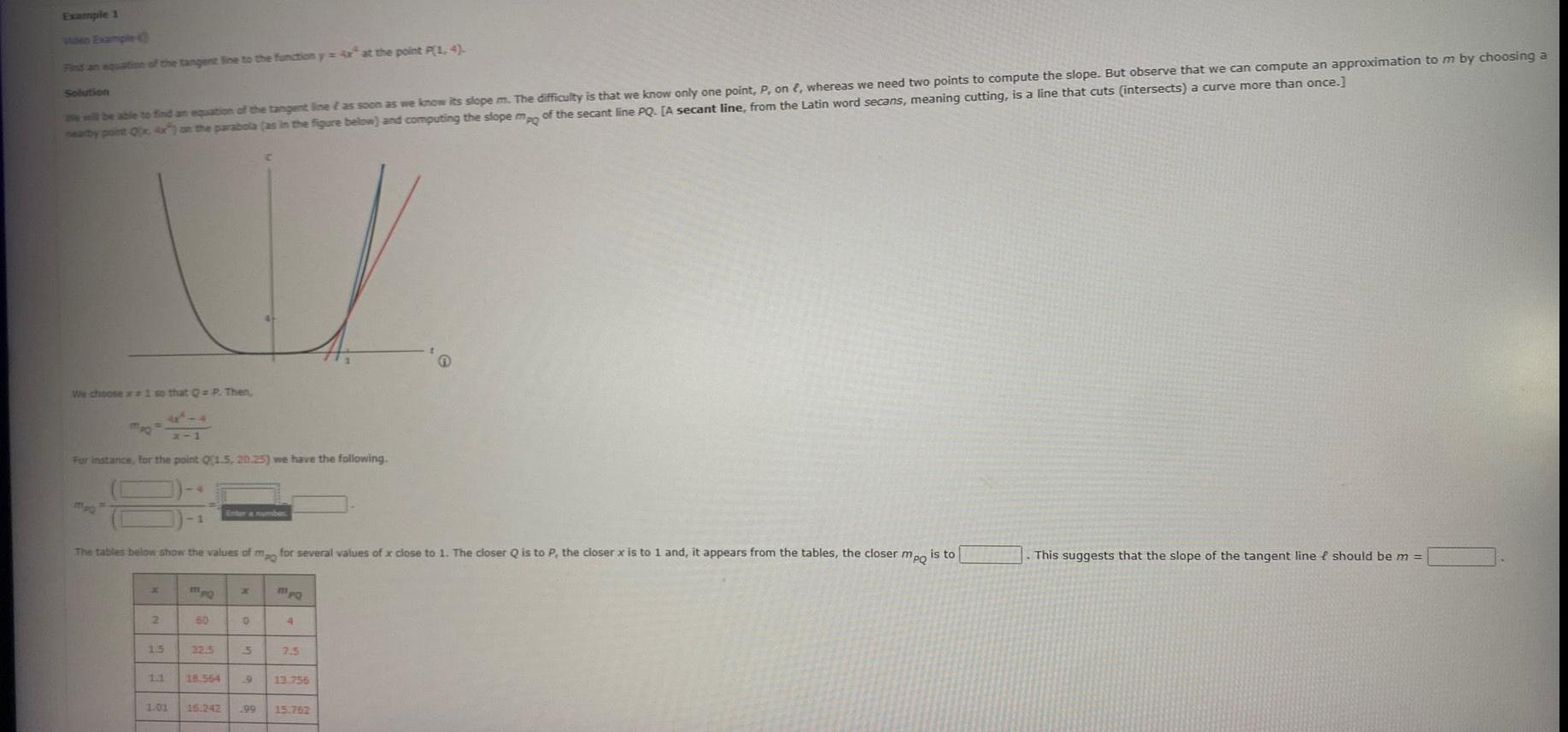
Example 1 Find an equation of the tangent line to the function y at the point P 1 4 Solution We will be able to find an equation of the tangent line as soon as we know its slope m The difficulty is that we know only one point P on whereas we need two points to compute the slope But observe that we can compute an approximation to m by choosing a nearby point Q x 4x on the parabola as in the figure below and computing the slope mpo of the secant line PQ A secant line from the Latin word secans meaning cutting is a line that cuts intersects a curve more than once We choose 1 so that Q P Then mpQ For instance for the point Q1 5 20 25 we have the following The tables below show the values of mo for several values of x close to 1 The closer Q is to P the closer x is to 1 and it appears from the tables the closer mpo is to x 2 1 5 1 1 MpQ 50 32 5 18 564 0 5 1 01 16 242 199 MpQ 4 7 5 13 756 15 762 This suggests that the slope of the tangent line f should be m