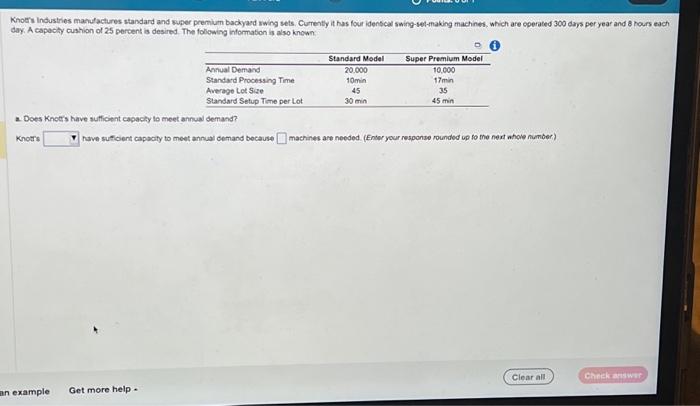
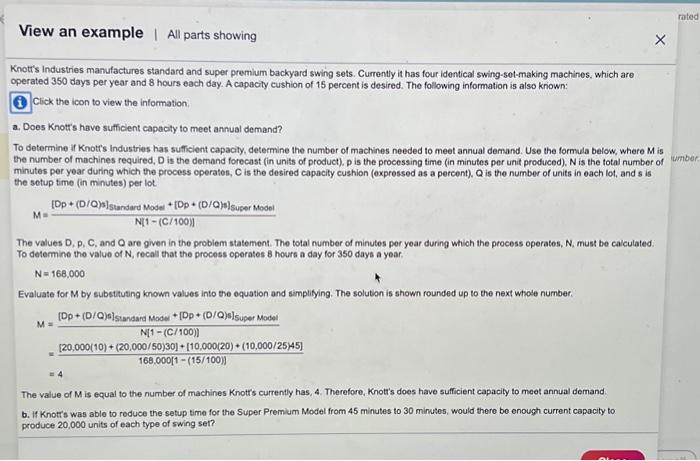
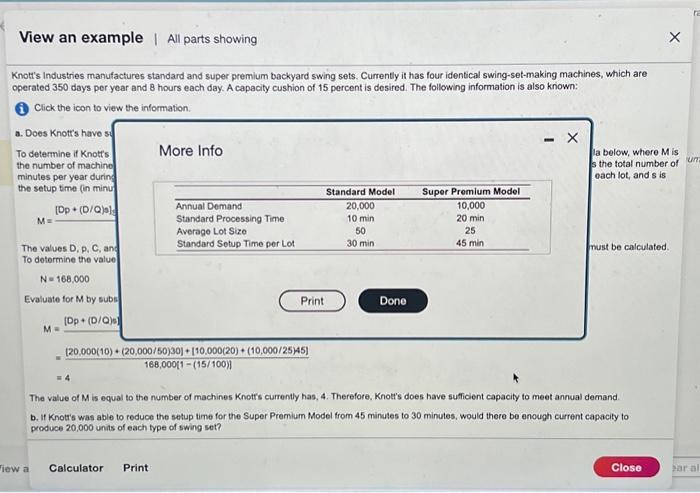
2. Does Knot's have sufficient capacily to meet annual demand? Knotrs have sutficient capacity to meet annual cemand because machines are needed. (Enter your response rounded up fo the next whole number) Knotr's Industries manufactures standard and super premium backyard swing sets. Currently it has four identical swing-sot-making machines, which are operated 350 days per year and 8 hours each day. A capacity cushion of 15 percent is desired. The following information is also known: Click the icon to view the information. a. Does Knotr's have sufficient capacity to meet annual demand? To determine if Knotrs Industries has sufficient capacity, determine the number of machines needed to meet annual demand. Use the formula below, where M is the number of machines required, D is the demand forecast (in units of product), p is the processing time (in minutes per unit produced), N is the total number of minutes per year during which the process operates, C is the desired capacity cushion (expressed as a percent), Q is the number of units in each lot, and s is the setup time (in minutes) per lot. M=N[1(C/100)][Dp+(D/Q)s]StandardModel+[Dp+(D/Q)s]SuperModel The values D,p,C, and Q are given in the problem statement. The total number of minutes per year during which the process operates, N, must be calculated. To determine the value of N, recall that the process operates 8 hours a day for 350 days a year. N=168,000 Evaluate for M by substituting known values into the equation and simplifying. The solution is shown rounded up to the next whole number. M=N[1(C/100)][Dp+(D/Q)s]StandardMode+[Dp+(D/Q)s]SuperModel=168,000[1(15/100)][20,000(10)+(20,000/50)30]+[10,000(20)+(10,000/25)45]=4 The value of M is equal to the number of machines Knotr's currently has, 4 . Therefore, Knott's does have sufficient capacity to meet annual demand. b. If Knotr's was able to reduce the setup time for the Super Premium Model from 45 minutes to 30 minutes, would there be enough current capacity to produce 20,000 units of each type of swing set? The values D, p, C, and Q are given in the problem statement. The total number of minutes per year during which the process operates, N, must be calculated. To determine the value of N, recall that the process operates 8 hours a day for 350 days a year. N=168,000 Evaluate for M by substituting known values into the equation and simplifying. The solution is shown rounded up to the next whole number: M=N[1(C/100)][Dp+(D/Q)s]StandardModel+[Dp+(D/Q)s]SuperModel=168,000[1(15/100)][20,000(10)+(20,000/50)30]+[10,000(20)+(10,000/25)45]=4 The value of M is equal to the number of machines Knotr's currently has, 4 . Therefore, Knotf's does have sufficient capacity to meet annual demand. b. If Knotts was able to reduce the setup time for the Super Premium Model from 45 minutes to 30 minutes, would there be enough current capacity to produce 20,000 units of each type of swing set? To determine if there would be enough current capacity to produce 20,0 do units of each type of swing set, once again, use the formula for M. This time reduce the setup time for the Super Premium Model from 45 minutes to 30 minutes and increase the demand for the Super Premium Model to 20,000 . The solution is shown rounded up to the next whole number. M=N[1(C/100)][Dp+(D/Q)s]standardModel+[Dp+(D/Q)s]SuperModel=168,000[1(15/100)][20,000(10)+(20,000/50)30]+[20,000(20)+(20,000/25)30]=5 5 The value of M is greater than the number of machines Knott's currently has, 4 . Therefore, Knotr's would not have enough capacity to produce 20,000 units of each type of swing sot. Knott's Industries manufactures standard and super premium backyard swing sets. Currently it has four identical swing-set-making machines, which are operated 350 days per year and 8 hours each day. A capacity cushion of 15 percent is desired. The following information is also known: Click the icon to view the information. a. Does Knotrs have sid To determine if Knott's More Info the number of machine minutes per year durind the setup time (in minu) M=[Dp+(D/Q)s] The values D,P,C, and To determine the value N=168,000 Evaluate for M by subs M=[Dp+(D/Q)s]=168,000[1(15/100)][20,000(10)+(20,000/50)30]+[10,000(20)+(10,000/25)45]=4 The value of M is equal to the number of machines Knotr's currently has, 4 . Therefore, Knotr's does have sufficient capacity to meet annual demand. b. If Knotr's was able to reduce the setup time for the Super Premium Model from 45 minutes to 30 minutes, would there be enough current capacity to produce 20,000 units of each type of swing set