example of format for substitution method:

with solution:

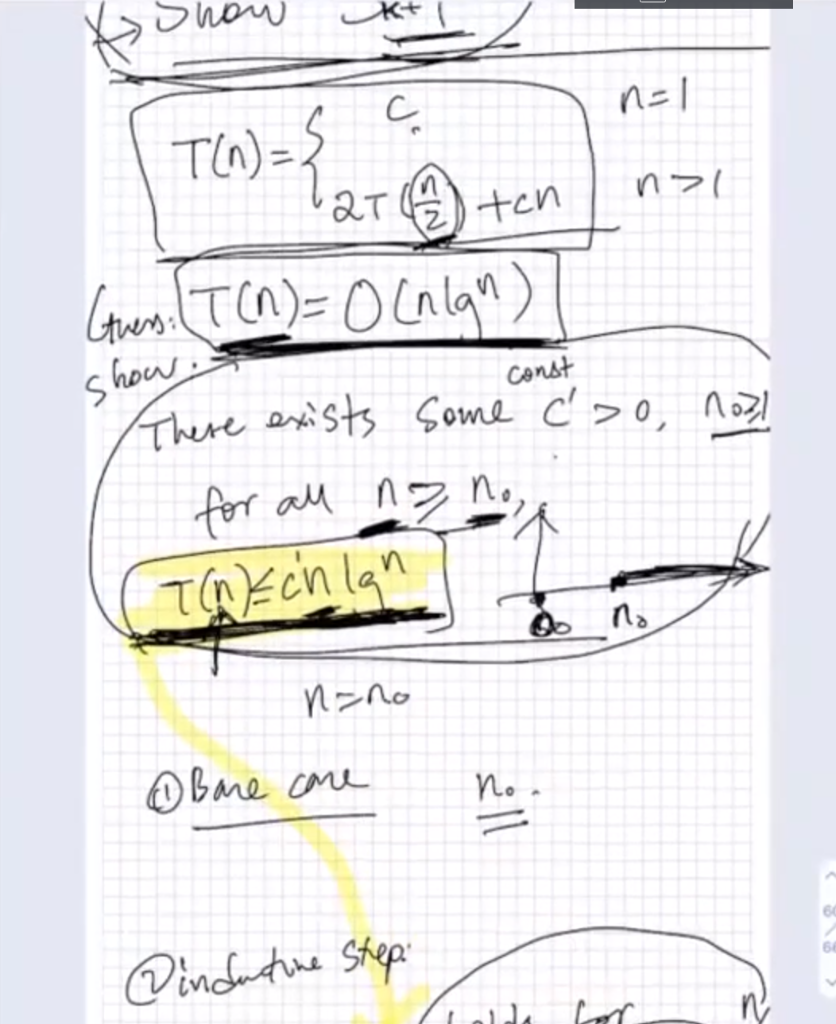
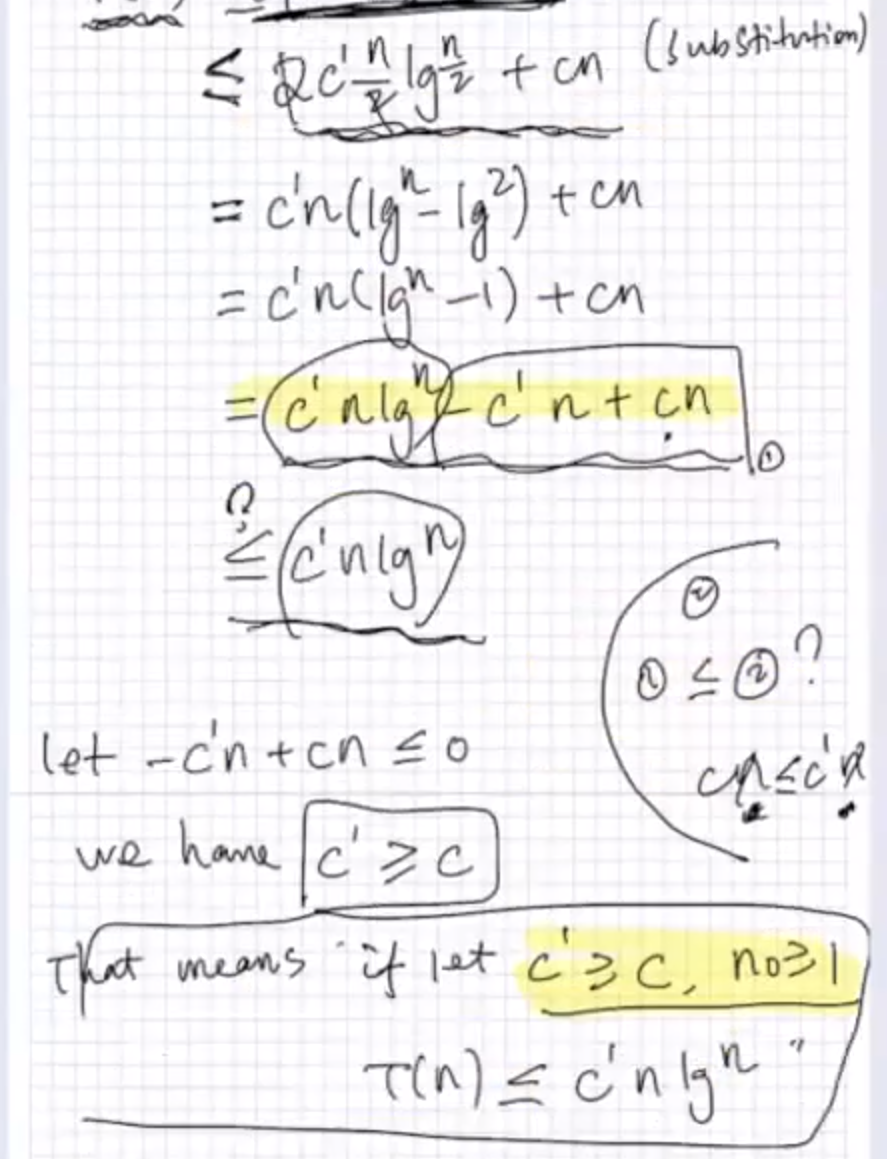
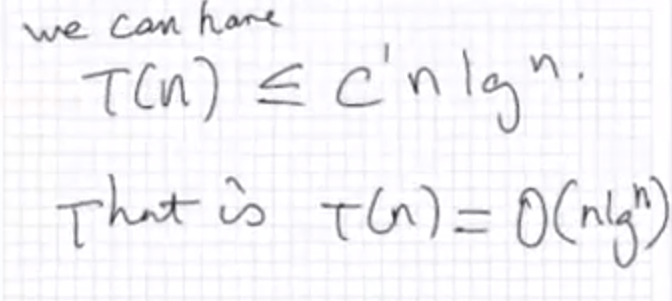
1. (15 pts) For the following recurrence, T(n) = 0 n = 1 T(n) = 4T(n-1) + c n>1 b. Use the substitution method to prove your above solution is correct. Show your work in sufficient details. Solving Recurrences with the Substitution Method (two steps): o Guess a solution Show the solution is correct by inductive proof. 1. Solve T(n) = c for n = 1 and T(n) = 2T(n/2) + cn for n> 1 using substitution. Guess: T(n) = O(nlgn). (We want to make a good guess - Is it a good guess?) Proof by Induction: 1) Goal: 2) Inductive Proof: Inductive Hypo: So far the restrictions (on C and no) are: 3) Base case: C n=1 TN-3 nal ten const Gws. T (n)= 0 (nlan2 There exists Some c'>o, nool for all na no TnEchlan show. n=no Bare care no no. @inductine Step: for @indutine step: Assume, holds for Smaller n (Stay Strong induting C C n=1 n> T(n)= 12T (AL) + en 1) Make a greens (through () 0 (nigh) the haurien tree). .S 2) show the quers That is show, 3c 20, noo, st. for au no no, T(n) = c'nign the the inductive Proof to show this -Induction Step T(A) Assume it holds for / That is Thus T(A) = c'h lg (hypo ) (n) = 21 (44) + cn (substitution) tch light on = c'h (Igh - lg ) = c'ncign-1) +on =c'algfcnten crigny 0 @? ( let -cntcn co casca we have c'>c That means if let c's C, nos T(n) = c'high" no So far, the restrictions on C and are c'>c, noI F let's verify whether Toh) = chign for n=1 Bare come and the values for cand no TUO =C, nos I No! ! verity for n=2 T(2) = 2T (1) + en = 2C +2C 2 = 40 s c'alg? That is A c pc ' 202C 2 cac Combining the two steps we can have let c'72c, no 32 T(n) = c'nlign we can have T(n) C'nign. That is th) = 0 (nigh)