Question
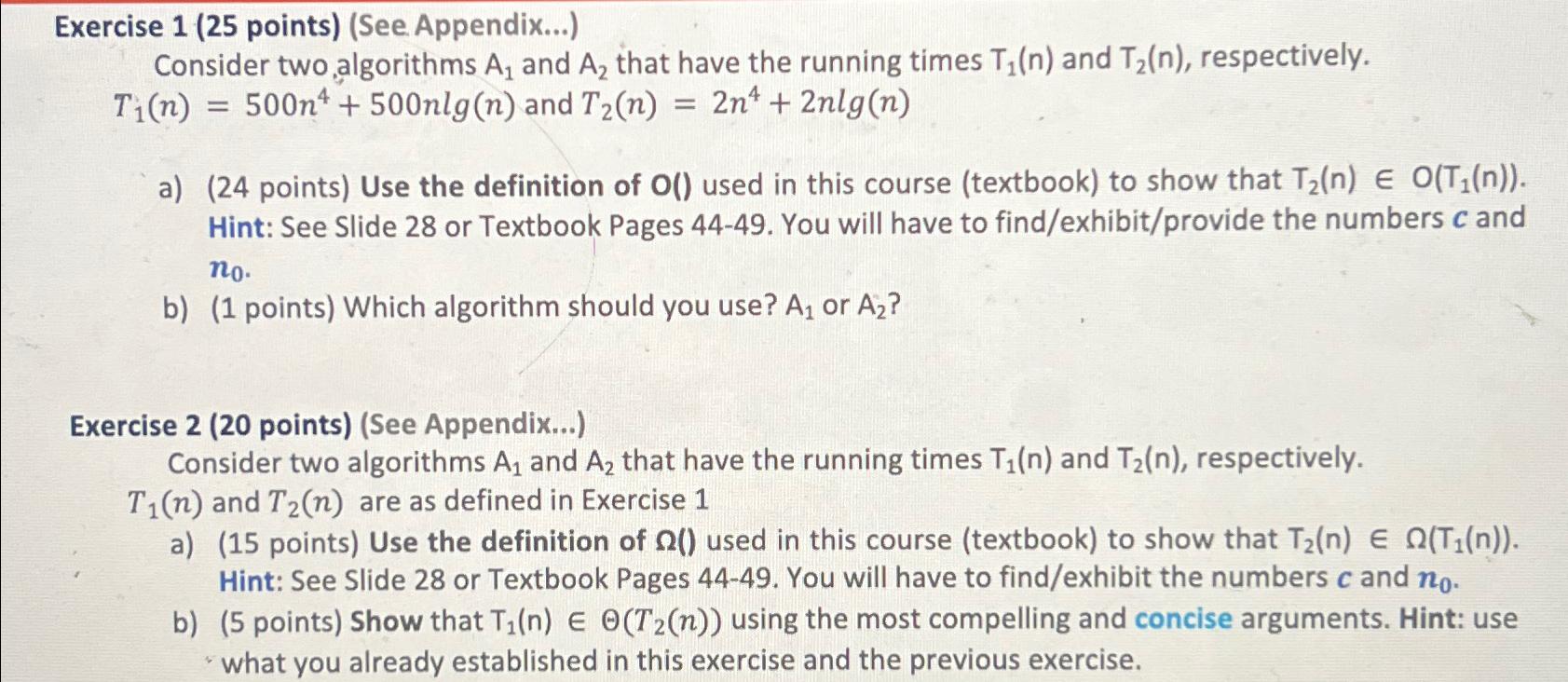
Exercise 1 ( 25 points) (See Appendix...) Consider two algorithms A_(1) and A_(2) that have the running times T_(1)(n) and T_(2)(n) , respectively. T_(1)(n)=500n^(4)+500nlg(n) and
Exercise 1 ( 25 points) (See Appendix...)\ Consider two algorithms
A_(1)and
A_(2)that have the running times
T_(1)(n)and
T_(2)(n), respectively.\
T_(1)(n)=500n^(4)+500nlg(n) and T_(2)(n)=2n^(4)+2nlg(n)\ a) (24 points) Use the definition of
O()used in this course (textbook) to show that
T_(2)(n)inO(T_(1)(n)). Hint: See Slide 28 or Textbook Pages 44-49. You will have to find/exhibit/provide the numbers
cand
n_(0).\ b) (1 points) Which algorithm should you use?
A_(1)or
A_(2)?\ Exercise 2 (20 points) (See Appendix...)\ Consider two algorithms
A_(1)and
A_(2)that have the running times
T_(1)(n)and
T_(2)(n), respectively.\
T_(1)(n)and
T_(2)(n)are as defined in Exercise 1\ a) (15 points) Use the definition of
\\\\Omega ()used in this course (textbook) to show that
T_(2)(n)in\\\\Omega (T_(1)(n)). Hint: See Slide 28 or Textbook Pages 44-49. You will have to find/exhibit the numbers
cand
n_(0).\ b) ( 5 points) Show that
T_(1)(n)in\\\\Theta (T_(2)(n))using the most compelling and concise arguments. Hint: use what you already established in this exercise and the previous exercise.
Step by Step Solution
There are 3 Steps involved in it
Step: 1

Get Instant Access to Expert-Tailored Solutions
See step-by-step solutions with expert insights and AI powered tools for academic success
Step: 2

Step: 3

Ace Your Homework with AI
Get the answers you need in no time with our AI-driven, step-by-step assistance
Get Started


