Exercise 1: Read both the introduction to the section and Example 1 (p. 969 - 971). Explain what the differential ds is substituted with in the computation of the line integral here. The subsection "Additivity" (p. 971 - 972) covers an important point when we have a sharp corner in our curve in a line integral. We add the two separate line integrals along each segment to deal with that corner. This notion of additivity extends to line integrals over vector fields which we will introduce in the next section. This notion is important for the same reason as here. Lastly, we have formulas for mass and the center of mass (along with moments of inertia) for a string or wire in space. This will be our main example for this type of line integral.

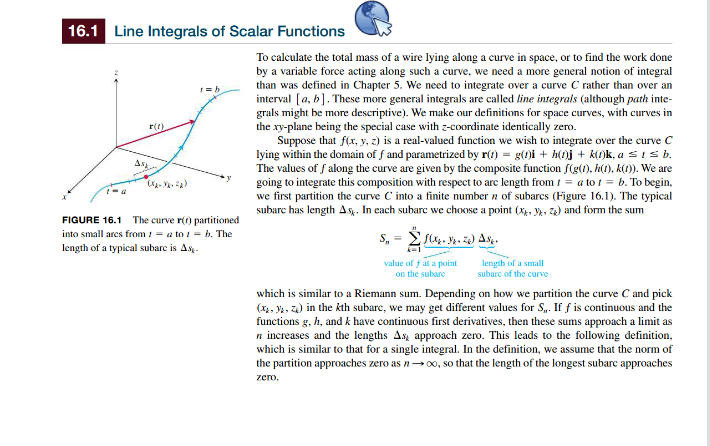
Chapter 16 Integrals and Vector Fields 16 Integrals and Vector Fields OVERVIEW In this chapter we extend the theory of integration to general curves and sur- faces in space. The resulting line and surface integrals give powerful mathematical tools for science and engineering. Line integrals are used to find the work done by a force in moving an object along a path, and to find the mass of a curved wire with variable density. Surface integrals are used to find the rate of flow of a fluid across a surface and to describe the interactions of electric and magnetic forces. We present the fundamental theorems of vector integral calculus, and discuss their mathematical consequences and physical appli- cations. The theorems of vector calculus are then shown to be generalized versions of the Fundamental Theorem of Calculus.16.1 Line Integrals of Scalar Functions To calculate the total mass of a wire lying along a curve in space, or to find the work done by a variable force acting along such a curve, we need a more general notion of integral than was defined in Chapter 5. We need to integrate over a curve C rather than over an interval [ a, b ]. These more general integrals are called line integrals (although path inte- grals might be more descriptive). We make our definitions for space curves, with curves in the xy-plane being the special case with z-coordinate identically zero. Suppose that f(x, y, 2) is a real-valued function we wish to integrate over the curve C lying within the domain of f and parametrization(ni + h(j + k(Q)ka s t s b. The values of f along the curve are given by the composite function f(e(0). h(), A(m)). We are going to integrate this composition with respect to are length from r = a to f = b. To begin. - a we first partition the curve C into a finite number a of subares (Figure 16.1). The typical subare has length As. In each subare we choose a point (1, ), 2) and form the sum FIGURE 16.1 The curve r(f) partitioned into small ares from / = a to 1 = b. The length of a typical subare is 4.- value of fat a point length of a small on the subare subarc of the curve which is similar to a Riemann sum. Depending on how we partition the curve C and pick (x, ), 2) in the kth subare, we may get different values for S,. If f is continuous and the functions g. h, and & have continuous first derivatives, then these sums approach a limit as " increases and the lengths As approach zero. This leads to the following definition. which is similar to that for a single integral. In the definition, we assume that the norm of the partition approaches zero as n -co, so that the length of the longest subare approaches zero.970 Chapter 16 Integrals and Vector Fields DEFINITION If f is defined on a curve C given parametrically by r(() = got)i + h(nj + k(r)k, a = = = b, then the line integral of f over C is fix, y. z) as = lim >f(r, MR. 2) Ask, (1) provided this limit exists. If the curve C is smooth for a = 1 = b (so v = dr/di is continuous and never 0) and the function f is continuous on C, then the limit in Equation (1) can be shown to exist. We can then apply the Fundamental Theorem of Calculus to differentiate the are length equation, Ey. (3) of Section 13.3 with 4 = a to express as in Equation (1) as ds = | v(n) | dr and evaluate the integral of f over C as + (2) The integral on the right side of Equation (2) is just an ordinary definite integral, as defined in Chapter 5, where we are integrating with respect to the parameter f. The for- mula evaluates the line integral on the left side correctly no matter what smooth parametric zation is used. Note that the parameter / defines a direction along the path. The starting point on C is the position r(a). and movement along the path is in the direction of increase ing ? (see Figure 16.1).How to Evaluate a Line Integral To integrate a continuous function /(r, y, z) over a curve C 1. Find a smooth parametrization of C. frio = NO, KO,KO) r(t) = gum)i + hoj + kok, asisb. 2. Evaluate the integral as f(x, y, z) ds =/ f(gin. h(t), kim|v()| dt. C (1. 1, 1) C If f has the constant value 1, then the integral of f over C gives the length of C from 1 = a to t = b. We also write f(r()) for the evaluation f(g(0, h(), k()) along the curve r. (1. 1, 0) EXAMPLE 1 Integrate f(x, y. z) = x - 3y' + z over the line segment C joining the origin to the point (1, 1, 1) (Figure 16.2). FIGURE 16.2 The integration path in Example 1. Solution Since any choice of parametrization will give the same answer, we choose the simplest parametrization we can think of: ro = / + + k, OSIEL.16.1 Line Integrals of Scalar Functions 971 The components have continuous first derivatives and (v()) = |i + j + k| = VP' + 1' + 12 = V3 is never 0, so the parametrization is smooth. The integral of f over C is Eq- (2), ds = [vi)| di = V3 dr =( ( - 32 + 1)V3dt = V3/ (21 - 37)d = V3 2 -1= Additivety Line integrals have the useful property that if a piecewise smooth curve C is made by join- ing a finite number of smooth curves Ci, C2, . ... G, end to end (Section 13.1), then the integral of a function over C is the sum of the integrals over the curves that make it up: (3)(1, 1, 1) EXAMPLE 2 Figure 16.3 shows another path from the origin to (1, 1, 1), formed from two line segments C, and C2- Integrate f(x, y, z) = x - 3y> + z over C U C. Solution We choose the simplest parametrizations for C and C we can find, calculat- (0. 0, 0) ing the lengths of the velocity vectors as we go along: C: r(() = + j, 0sis I; v) = VP+ P = v2 G: r()=itj+k. 0=/=1; v = Vo+0' + 1' =1. (1, 1, 0) With these parametrizations we find that FIGURE 16.3 The path of integration in Example 2. for. y. Dids = / fix.y. Dids + / fix.y. D)ds Eg. (3) Ey. (2) 2 Notice three things about the integrations in Examples 1 and 2. First, as soon as the components of the appropriate curve were substituted into the formula for f, the integra- tion became a standard integration with respect to t. Second, the integral of f over G U Cz was obtained by integrating f over each section of the path and adding the results. Third, the integrals of f over C and C U C, had different values. We investigate this third obser vation in Section 16.3.972 Chapter 16 Integrals and Vector Fields The value of the line integral along a path joining two points can change if you change the path between them. EXAMPLE 3 Find the line integral of ((x, y. z) = 2xy + V'z over the helix r(1) = cos /i + sin ij + k. O = IST. Solution For the helix (Figure 16.4) we find v(?) = r'(t) = -sinti + costj + k and |v(b)|= V(-sinn- + ( cost) + 1 = V2. Evaluating the function f at the point r(t), we obtain f(r()) = f(cost, sin t. 1) = 2 cos / sin / + V/ = sin 2 + VT. The line integral is given by [ fax.2)ds = / (sin 2 + Vi) Vid FIGURE 16.4 A line integral is taken over a curve such as this helix from = v2 -ons 2+ + 13/27 Example 3. 2V/2 3 ETT 3/2 =6 5.25. Mass and Moment Calculations We treat coil springs and wires as masses distributed along smooth curves in space. The distribution is described by a continuous density function S(x, y, z) representing mass per unit length. When a curve C is parametrization()j + z(t)k, a st s b, then x, y, and z are functions of the parameter , the density is the function S(x(), y(), z()), and the arc length differential is given by dix dy dz dt di.(See Section 13.3.) The spring's or wire's mass, center of mass, and moments are then calculated using the formulas in Table 16.1, with the integrations in terms of the parameter f over the interval [a, b] . For example, the formula for mass becomes M = dr. These formulas also apply to thin rods, and their derivations are similar to those in Section 6.6. Notice how alike the formulas are to those in Tables 15.1 and 15.2 for double and triple inte- grals. The double integrals for planar regions, and the triple integrals for solids, become line integrals for coil springs, wires, and thin rods. Notice that the element of mass do is equal to 8 ds in the table rather than 6 dV as in Table 15.1, and that the integrals are taken over the curve C. (I. F. The center of mass EXAMPLE 4 A slender metal arch, denser at the bottom than top. lies along the semicircle y- + 2' = 1.z >: 0. in the yz-plane (Figure 16.5). Find the center of the arch's mass if the density at the point (x, y, z) on the arch is 8(x, y. z) = 2 - z. X +=1:20 Solution We know that I = 0 and y = 0 because the arch lies in the yz-plane with its FIGURE 16.5 Example 4 shows how to mass distributed symmetrically about the z-axis. To find Z, we parametrizations find the center of mass of a circular arch of variable density. r(m) = (cos n)) + (singk. OSIST