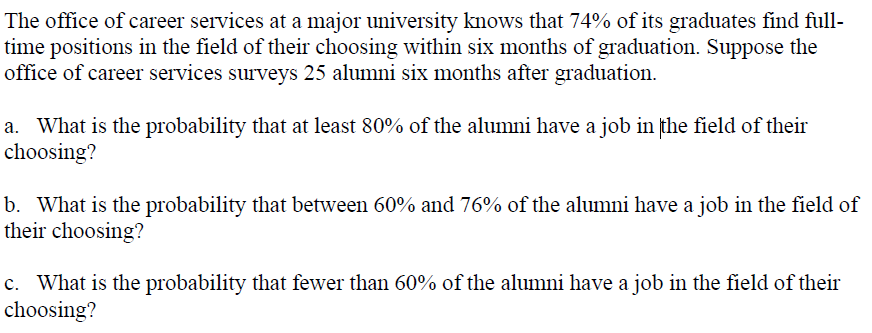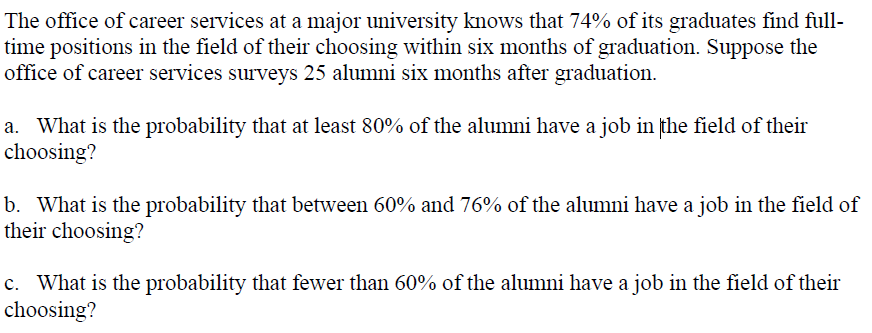
Exercise 1

The Japan Sumo Association has begun to measure the body fat of wrestlers to try to combat the growing problem of excessive obesity within the sport. As of last year, the average wrestler weighed 412 pounds. Suppose the weights of sumo wrestlers are normally distributed, with a standard deviation of 37 pounds. What is the probability that a randomly selected wrestler weighs between 350 and 450 pounds?A book publisher knows that it takes an average of nine business days from when the material for the book is finalized until the first edition is printed and ready to sell. Suppose the exact amount of time has a standard deviation of four days. a. Suppose the publisher examines the printing time for a sample of 36 books. What is the probability that the sample mean time is shorter than eight days? b. Suppose the publisher examines the printing time for a sample of 36 books. What is the probability that the sample mean time is between 7 and 10 days? c. Suppose the publisher signs a contract for the printer to print 100 books. If the average printing time for the 100 books is longer than 9.3 days, the printer must pay a penalty. What is the probability the penalty clause will be activated? d. Suppose the publisher signs a contract for the printer to print 10 books. If the average printing time for the 10 books is longer than 9.7 days, the printer must pay a penalty. What is the probability the penalty clause will be activated?The office of career services at a major university knows that 74% of its graduates find full- time positions in the field of their choosing within six months of graduation. Suppose the office of career services surveys 25 alumni six months after graduation. a. What is the probability that at least 80% of the alumni have a job in the field of their choosing? b. What is the probability that between 60% and 76% of the alumni have a job in the field of their choosing? c. What is the probability that fewer than 60% of the alumni have a job in the field of their choosing?Administrative assistants in a local university have been asked to prove their proficiency in the use of spreadsheet software by taking a proficiency test. Historically, the mean test score has been 74 with a standard deviation of 4. A random sample of size 40 is taken from the 100 administrative assistants and asked to complete the proficiency test. a. Calculate the expected value and the standard deviation (standard error) of the sample mean. b. What is the probability that the sample mean score is more than 75, the predetermined passing score